Der unglaubliche Quantencomputer einfach erklärt

<<   >>

Durch Quantencomputer wird die rätselhafte Quantenmechanik dafür genutzt, um völlig neuartige berechnende Systeme bereit zustellen. Deshalb besitzen Quantencomputer Eigenschaften die schier unglaublich wirken: So steigert sich die Leistungsfähigkeit eines Quantencomputers zum Beispiel „exponentiell“, also quasi explosionsartig, mit zunehmender Größe. Im Folgenden erkläre ich Ihnen in einfachen Worten diese besonderen Eigenschaften eines Quantencomputers und gehe genauer auf die erstaunlichen Quantenprogramme ein.

Der Paukenschlag: Der Shor-Algorithmus

Im Jahr 1994 hatte der Mathematiker Peter Shor vom renommierten Massachusetts Institute of Technology / MIT die Idee seines Lebens. Eine Idee, die eine neue Ära einleiten würde.

Shor untersuchte ein neues Verfahren, um eine ganze Zahl in Primzahlen zu zerlegen. Diese Primzahlfaktorisierung ist eine extrem aufwendige Angelegenheit. Um sehr großen Zahlen in Primzahlen zu zerlegen, brauchen selbst sehr leistungsstarke Supercomputer mehrere Jahre. ⁱ

Unter anderem deshalb wird sie für die sichere Datenverschlüsselung im Internet verwendet. Es ist zwar sehr einfach selbst große Zahlen aus bekannten Primzahlen zusammenzusetzen (z.B. 7×13×13×17×53 = 1065883). Da die Umkehrung aber nahezu unmöglich ist, ist die Verschlüsselung im Internet bombensicher.

Eigentlich!

Shor fragte sich, ob man das neue Verfahren nutzen könnte, um neue Algorithmen für die Primzahlzerlegung zu erstellen. Irgendwann erinnerte er sich an eine Pflichtvorlesung über Quantenmechanik, die er seinerzeit als Mathematik-Student noch am California Institute of Technology (Caltech), hatte hören müssen. Ihm kam die grandiose Idee, dass das Verfahren ungleich schneller zum Ziel führen könnte, wenn man zur Berechnung nicht einen herkömmlichen Computer, sondern einen Quantencomputer verwenden würde. Er tüfftelte ein Jahr an seinem Quanten-Algorithmus und kam am Ende tatsächlich zu dem gewünschten Ergebnis ⁱⁱ.

Shors Algorithmus schlug ein wie eine Bombe. Bis zu diesem Zeipunkt, war es noch niemanden gelungen einen Quantencomputer zu konstruieren. Der Shor-Algorithmus war aber der erste Beweis, wie ungeheuer leistungsstark ein Quantencomputer sein und welche gesellschaftlichen Auswirkungen er haben würde. Shors Algorithmus löste einen regelrechten Boom in den Quantencomputer-Szene aus.

Ein Quantencomputer macht sich die außergewöhnlichen Eigenschaften der atomaren Welt zu nutze, um über spezielle Quantenprogrammen, den Quanten-Algorithmen, ganz neue Dimensionen in der Rechengeschwindigkeit zu erzielen. Das Wort „außergewöhnlich“ ist hierbei wohl noch untertrieben. Die Quantenwelt ist eine rätselhafte Welt mit schon fast magischen Eigenschaften.

Um einen Eindruck davon zu bekommen, was das Besondere an einem Quantencomputer ist, müssen wir uns erst einmal anschauen, wie ein herkömmlicher Computer funktioniert.

Einfach erklärt: Wie funktioniert ein herkömmlicher Computer?

Nehmen wir Ihren Computer, mit dem Sie diese Zeilen lesen. Er steuert Informationen in Form von Nullen und Einsen über Bits bzw. Bytes an. Die Zahl „71“ wird z.B. durch die Bit-Reihe „0100 0111“ dargestellt und der Buchstabe „J“, per Konvention, durch die Bit-Reihe „100 1010“. Ihr Computer merkt sich, ob eine Bit-Reihe eine Zahl, einen Buchstaben, ein Bild oder Musik darstellt. Die Bits selbst existieren in Form von Milliarden elektrischer An / Aus – Schalter, den Transistoren. Zusammen bilden sie den Arbeitsspeicher Ihres Computers. Ein guter herkömmlicher Computer besitzt etwa 16 * 8 Milliarden Bits oder anders ausgedrückt: 16 Gigabyte. Ein Computerprogramm manipuliert diese Bits in einzelnen Rechenschritten über die elementarsten Bausteine der menschlichen Logik: UND-Verknüpfungen, ODER-Verknüpfungen, NICHT-Verknüpfungen. Diese Verknüpfungen werden auch „Gatter“ genannt (englisch gates). Eine NICHT-Verknüpfung kehrt ein einzelnes Bit z.B. in sein Gegenteil um: NICHT 0 = 1, NICHT 1 = 0 .

Über geschickte elektrische Schaltungen, dem Datenbus, ist Ihr Computer in der Lage jedes der unzähligen Bits im Arbeitsspeicher gezielt anzusteuern, auszulesen oder mit neuen Werten zu überschreiben. Ein Rechenschritt sieht dann zum Beispiel so aus:

„Lese den Wert des Bits mit der Adress-Nummer 1543216 und den Wert des Bits mit der Adress-Nummer 6543 aus und verknüpfe beide Werte mit einem UND-Befehl. Speicher das Ergebnis im Bit mit der Adress-Nummer 789874“. Durch eine geschickte Hintereinanderreihung dieser elementaren UND-, ODER-, NICHT-Verknüpfungen ist Ihr Computer zum Beispiel in der Lage zwei Zahlen miteinander malzunehmen. Nach jedem einzelnen dieser Rechenschritte schreibt Ihr Computer die Zwischenergebnisse wieder in den Arbeitsspeicher hinein und ruft sie von dort wieder für den nächsten Rechenschritt auf. Das Programm für das Mal-Nehmen sieht unnötig umständlich und mechanisch stupide aus. Da Ihr Computer aber in der Lage ist Milliarden von Rechenschritten pro Sekunde auszuführen ist er jedem Menschen am Ende in solchen Aufgaben gigantisch überlegen.

Die Qubits einfach erklärt

Ein Quantencomputer steuert im Gegensatz dazu die Informationen nicht über einfache An / Aus-Schalter an, also den herkömmlichen Bits, sondern über sogenannte „Qubits“ (für Quanten-Bits). In einem Qubit sind die Werte 0 / 1 bzw. An / Aus gleichzeitig in einer überlagerten Form vorhanden. Das sieht auf den ersten Blick vielleicht harmlos aus. Tatsächlich ist diese Überlagerung eines der großen Rätsel der Quantenmechanik.

Als Konsequenz ersann der österreichische Nobelpreisträger Erwin Schrödinger vor fast hundert Jahren sein berühmtes Gedankenexperiment „Schrödingers Katze“: Eine Katze, die zusammen mit einem Qubit überlagert ist. Das Qubit schaltet einen Giftcocktail ein, sobald es den Wert 1 hat. Wenn das Qubit aber gleichzeitig den Wert 0 und den Wert 1 besitzt, so Schrödinger, müsste die Katze ebenfalls gleichzeitig tot und lebendig sein.

In meinem Artikel „Das Qubit und ein Magier bei Britain Has Got Talent“ vergleiche ich das Qubit mit einem spektakulären Zaubertrick des Magiers Darcy Oake in der englischen Talentshow von 2014. Darin steht Darcy Oake scheinbar zweimal gleichzeitig auf der Bühne. Ein Qubit verhält sich genauso. Allerdings nicht als Trick, sondern in Wirklichkeit.

Um dies zu veranschaulichen, verwende ich auf „quantencomputer-info.de“ eine Qubit-Darstellung, die gegenüber der Lehrbuchdarstellung vereinfacht ist aber dem Kern bereits sehr nahe kommt: Ein einfacher Zeiger in einer Ebene. Folgendes Qubit ist zum Beispiel zu gleichen Teilen sowohl im Zustand 0 als auch im Zustand 1.

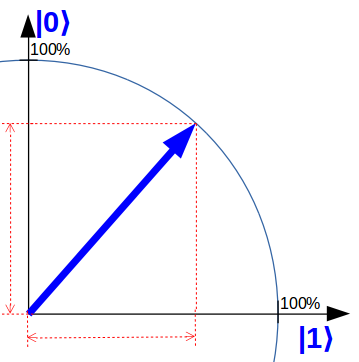
Wenn Sie jetzt denken: „Verstanden! Dann wären zwei Qubits einfach zwei Zeiger“, muss ich Sie leider enttäuschen. So einfach machen die Quantencomputer es uns dann doch nicht. Tatsächlich entsprechen zwei Qubits in der vereinfachten Darstellung immer noch einem Zeiger, allerdings mit vier jeweils senkrechten Achsen!

Ich weiß, jeder Versuch vier Dimensionen irgendwie bildlich darzustellen, endet kläglich. Ich will es trotzdem versuchen:

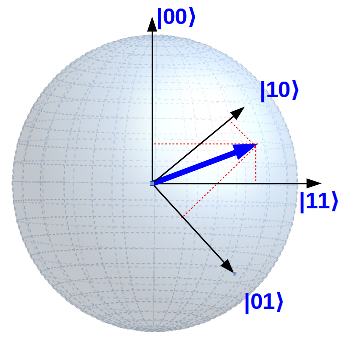
Sie können sich vorstellen, dass dieses Verhalten sehr ungewöhnliche Konsequenzen hat … Mehr dazu weiter unten in dem Abschnitt über die „Quanten-Verschränkung“.

Die zweite so außergewöhnliche Eigenschaft von Qubits ist die Folgende: Man kann einen Quantencomputer zwar sogar durch einen herkömmlichen Computer simulieren bzw. nachbilden (Probleme aus der Quantenmechanik lassen sich schließlich auch durch „herkömmliche“ Methoden berechnen), der Aufwand dafür nimmt mit steigender Qubitzahl allerdings schnell gigantische Ausmaße an. Die folgende Liste zeigt, wie viele herkömmliche Bits notwendig sind, um die entsprechende Menge an Qubits nachzubilden ⁱⁱⁱ .

• • • • 1 Qubit benötigt 256 herkömmliche Bits
      • 2 Qubits benötigen 512 herkömmliche Bits
      • 10 Qubits benötigen 16 herkömmliche kilo-Byte
      • 20 Qubits benötigen 16 herkömmliche Mega-Byte
      • 30 Qubits benötigen 16 herkömmliche Giga-Byte
      • 31 Qubits benötigen 32 herkömmliche Giga-Byte

Jedes weitere Qubit verdoppelt also die benötigte Anzahl von herkömmlichen Bits! Die Leistungsfähigkeit eines Quantencomputers steigt also im Vergleich exponentiell! Und so geht’s weiter:

• • • 45 Qubits benötigen in etwa der Speichergröße des größten aktuellen, herkömmlichen Supercomputers

• • • 50 Qubits, die „Quanten-Überlegenheit“-Grenze: Die Grenze an dem ein Quantencomputer gewisse Berechnungen durchführen kann, die mit keinem der aktuellen Supercomputer durchführbar sind ^iv. Mehr dazu in meinem Artikel „Googles Nachweis der Quanten-Überlegenheit“ 

• • • 250 Qubits: Die absolute Grenze, die überhaupt machbar wäre für herkömmliche Computer. Um einen 250 Qubit-Quantencomputer nachzubilden, müsste ein herkömmlicher Computer jedes Atom im Universum als herkömmliches Bit verwenden.

Das wirkt unglaublich. Ist es auch!

Und nun bedenken Sie mal, dass die Quantencomputer-Hersteller das Ziel haben irgendwann einmal Quantencomputer mit Millionen von Qubits zu bauen!

Quantencomputer einfach erklärt: Quantenparallelismus, Superposition

Der Clou bei diesen ungeheuren Zahlen ist aber tatsächlich Folgender: Nehmen wir nochmal das Beispiel mit dem Mal-Nehmen. Ihr herkömmlicher Computer nimmt zwei Zahlen, in Form von zwei Bit-Reihen im Arbeitsspeicher, führt das festgelegte Programm von einzelnen Rechenschritten aus und erhält am Ende eine Zahl in Form von einer Bit-Reihe.

Ein Quantencomputer nimmt im Gegensatz dazu für eine Aufgabe zwei Qubit-Reihen, speichert die Zwischenergebnisse wieder in Qubits und erhält am Ende das Ergebnis in Form einer Qubit-Reihe ^v. Da in einer Qubit-Reihe aber riesige Mengen von Informationen gleichzeitig enthalten sein können (s.o.), kann der Quantencomputer das Programm letztendlich gleichzeitig mit einer riesigen Menge von Zahlen ausführen. Dies ist der Quantenparallelismus. Normalerweise spricht man aber von der „Superposition“.

Tatsächlich gibt es diese Form von Überlagerung öfter in der Natur und nicht nur in der Quantenmechanik ^vi. Was den Quantenparallelismus so besonders macht ist die Tatsache, dass nur wenige Qubits so unvorstellbar große Datenmengen überlagern können. Die Qubits werden nämlich nicht nur einzeln überlagert, sondern der gesamte Verbund an Qubits. Und gerade dabei erhöht sich die Anzahl von möglichen Kombination so rasant. Für drei Qubits werden also z.B. bis zu acht mögliche Bit-Zustände gleichzeitig verwendet (das entspricht 2³): Nämlich 000, 100, 001, 101, 011, 111, 010 und 110.

Aber: Jede Messung zerstört die Quanteneigenschaften

Die enorme parallele Rechenleistung eines Quantencomputers hat leider einen großen Haken: Sie funktioniert nur solange der Quantencomputer perfekt von seiner Umgebung isoliert ist und die höchst fragilen Qubits ungestört sind. Indem wir am Ende allerdings das Ergebnis des Quantenprogramms aus den Qubits auslesen, tun wir aber genau das. In diesem Moment „zerfallen“ die gleichzeitig vorhandenen Werte und übrig bleibt nur ein einziger Wert der darüber hinaus auch noch zufällig gewählt wird. Dieser Zerfall ist als „Kollaps der Wellenfunktion“ bekannt und ist noch so ein Mysterium der Quantenwelt. Er war der Grund, warum manche Physiker, unter ihnen selbst Albert Einstein, die Quantentheorie zwar schätzten und vorantrieben aber im Grunde ablehnten: „Gott würfelt nicht“.

Nebenbei: Für den Bau von Quantencomputern haben solche Störungen fast unlösbare Konsequenzen. Wie man Quanteneigenschaften trotzdem dagegen „schützen“ kann, und welche grundlegende Bedeutung diese „Quanten-Fehlerkorrektur“ sogar für die Natur von Raum und Zeit haben könnte, erläutere ich Ihnen im nächsten Artikel „Der sehr, sehr steile Weg zum ersten Quantencomputer“.

Und jetzt? Was ist überhaupt gewonnen, wenn am Ende doch nur alles vom Zufall abhängt?

Jetzt kommt das Aber: Die Wahrscheinlichkeiten, mit denen die verschiedenen Werte am Ende ausgelesen bzw. gemessen werden, können wir beeinflussen. Die Kunst eines Quantenprogramms besteht unter anderem darin, die Qubits so zu manipulieren, dass das gesuchte Ergebnis am Ende am Wahrscheinlichsten gemessen wird. Bis dahin, also während er noch von seiner Umgebung isoliert ist, kann dann die enorme Rechenkraft des ungestörten Quantencomputers genutzt werden.

Mehr über Quantenprogramme erfahren Sie weiter unten. Kommen wir zunächst zu einer der merkwürdigsten Eigenschaften von Quanten bzw. von Qubits.

Einsteins spukhafte Verschränkung

Oben hatte ich schon ein Zeigerbeispiel für zwei Qubits dargestellt. Diese Zeiger-Eigenschaft hat eine bizarre Konsequenz. Albert Einstein höchstpersönlich sagte sie 1935 in einem berühmten Aufsatz voraus: Die „Quanten-Verschränkung“ (engl. „entanglement“, er selbst bezeichnete das Phänomen auch „spukhafte Fernwirkung“). Wir können zwei Qubits (oder auch mehrere Qubits) derart überlagern, dass wir sie nicht mehr als einzelne Qubits erkennen können. Stattdessen bilden sie eine völlig neuartige, einheitliche Zustandsform. Sie erscheinen „verschränkt“: Eine Messung am ersten Qubit hat sofort Auswirkungen auf das zweite Qubit.

Um das zu verdeutlichen schauen wir uns nochmal ein Zeigerdiagramm mit 4 Achsen an. Der blaue Zeiger unten beschreibt den gemeinsamen Zustand von Qubit A und Qubit B. Jetzt führen wir eine Messung nur an Qubit B durch. Im vorigen Abschnitt haben Sie erfahren, dass sich Qubit B durch die Messung für einen Zustand entscheidet: Wir messen entweder den Zustand 0 oder den Zustand 1. An Qubit A haben wir noch keine Messung durchgeführt. Eigentlich müssten wir also für Qubit A einen einzelnen überlagerten Zeiger in zwei Dimensionen erhalten, der nichts über die vorangegangene und unabhängige Messung an Qubit B „weiß“.

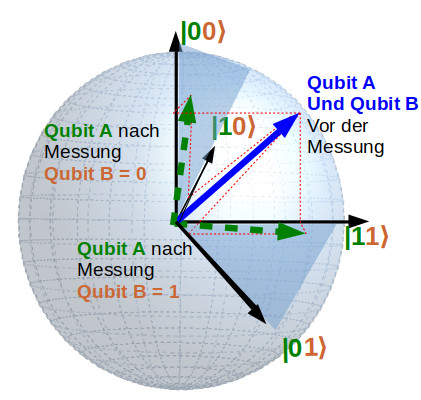
An dem Beispiel erkennen Sie aber, dass sich die Messung sehr wohl direkt auf Qubit A auswirkt. Qubit A ist nach der Messung so etwas wie der „Schatten“ des ursprünglichen blauen Zeigers, den ich durch die gestrichelten Zeiger andeute. Die Ebene, in der dieser Schatten liegt wird durch die Messung von Qubit B festgelegt: Wenn wir für Qubit B den Zustand 0 messen, erhalten wir für Qubit A den linken gestrichelten Zeiger, der hauptsächlich in die 0-Richtung zeigt. Wenn wir für Qubit B den Zustand 1 messen, erhalten wir für Qubit A den unteren gestrichelten Zeiger, der hauptsächlich in die 1-Richtung zeigt.

Ziel von Einsteins Arbeit war es tatsächlich, der Quantenmechanik einen grundlegenden Denkfehler nachzuweisen. Laut Einstein müsste diese verschränkte Einheit bestehen bleiben, selbst wenn die beiden Qubits Lichtjahre voneinander entfernt wären. Deshalb sprach er von Fernwirkung. Das Verrückte dabei ist: Alle Experimente deuten daraufhin, dass es genauso ist. Die Fernwirkung ist real in der Quantenwelt und sie wirkt sich sofort aus!

Solche verschränkten Zustandsformen gibt es nirgendwo sonst in den Naturwissenschaften. Vielleicht bis auf eine Ausnahme: Ein sogenanntes astronomisches „Wurmloch“, das zwei schwarze Löcher über eine Distanz von vielen Lichtjahren miteinander verbinden kann, als eine Art Hyper-Schnellstraße. Die Frage, wie diese beiden Phänomene zusammenhängen ist tatsächlich Gegenstand aktueller Forschung in der theoretischen Physik.

Quantengatter einfach erklärt: Die Bausteine der Quantenprogramme

Auf einem Quantencomputer können wir nicht einfach dieselben Algorithmen laufen lassen, die auf einem herkömmlichen Computer funktionieren. Stattdessen müssen wir für Quantencomputer vollkommen neue und fremdartige Quanten-Algorithmen konstruieren.

Dafür verwendet ein Quantencomputer in jedem Rechenschritt ebenfalls elementare Logik-Bausteine, den „Quantengattern“ (engl. quantum gates). Diese spiegeln allerdings nicht unsere normale Alltagslogik wieder, sondern die Quantenlogik: Somit heißen die elementaren Bausteine nicht mehr UND, ODER oder NICHT. Stattdessen verwendet ein Quantencomputer Logik-Bausteine die z.B. Hadamard, X, S, T, Z, Controlled NOT oder Controlled Z heißen. Diese Quantengatter ähneln in ihrer Funktionsweise weniger den bekannten Bausteine unserer Alltagslogik als vielmehr Drehungen in einem riesigen abstrakten „Hyperraum“ (oder genauer: ein „Hilbert“-Raum). Die Qubits bilden in ihrer Gesamtheit einen einzelnen Zeiger in diesem Raum, der durch jedes einzelne Quantengatter gedreht wird. Für zwei Qubits hatten Sie schon weiter oben einen Eindruck davon bekommen.

Diese grundlegende Fremdheit gegenüber unserer Alltagslogik ist der Grund, warum ein Quantenprogramm nur für Kenner von Quanten-Algorithmen entziffert und verstanden werden kann.

Für alle Darstellungen von Quantengatter-Schaltungen verwende ich auf „quantencomputer-info.de“ den exzellenten Quantencomputer-Simulator „Quirk“:

http://algassert.com/quirk

Quirk ist öffentlich erreichbar und kann direkt in Ihrem Browser ausprobiert werden (per „WebGL“). Craig Gidney, der Programmierer von Quirk, hat dabei ein eine Reihe bekannter Quanten-Algorithmen beispielhaft modeliert. Sie sollten dort unbedingt einmal reinschauen. Mein Favorit ist die „Quanten-Teleportation“, in der der Autor über eine Animation sehr schön verdeutlicht, wie sich ein Qubit-Zustand per Verschränkung über eine Distanz in ein zweites Qubit sprunghaft tele-transportieren lässt. Gidney ist mittlerweile übrigens bei Google angestellt und hat dort die Quanten-Programmierschnittstelle „Cirq“ federführend entwickelt.

In jedem Bereich der herkömmlichen Programmierung existiert eine lebhafte IT-Szene im Internet, die die weitere Entwicklung stark beeinflusst: Seien es Server, Netzwerke. Datenbanken, Internet, Programmierung, … Die IT-Szene für Quantenprogrammierung sitzt hauptsächlich noch in den Forschungseinrichtungen von Universitäten und hauptsächlich in den Spezialabteilungen von Google, IBM, Microsoft & Co und einigen Startups für Quantencomputer. Seit dem Frühjahr 2018 gibt es zwar das neue Diskussionsforum „Quantum Computing Stack Exchange“ ^vii, dass sich sehr lebhaft und inhaltlich hochwertig entwickelt. Wichtige Ergebnisse werden trotzdem weiterhin über komplizierte wissenschaftliche Arbeiten veröffentlicht.

Die wohl folgenreichste dieser Veröffentlichung war gerade der Algorithmus von Peter Shor aus dem Jahr 1994, der in der Lage ist, die als sicher geglaubte Datenverschlüsselung im Internet zu knacken. Mittlerweile wurden andere, rasend schnelle und vermutlich auch interessantere Quanten-Algorithmen konstruiert.

Beispiel von der Quirk-Homepage: Schematischer Aufbau des Shor-Algorithmus.

Alle Anbieter von Quantencomputern haben mittlerweile Programmierschnittstellen entwickelt. Über diese Schnittstellen können die Quanten-Programme entweder per Simulator auf dem eigenen PC oder vom eigenen PC aus per Fernsteuerung auf dem Cloud-Quantencomputer des Herstellers ausgeführt. Der folgende Programmauszug zeigt Googles Beispiel zum Shor-Algorithmus in Googles eigener Programmierschnittstelle „Cirq“.

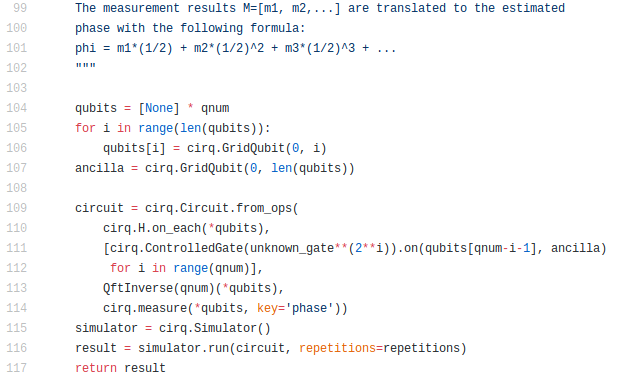
An diesen Beispielen erkennen Sie übrigens auch, wie sehr die Quanten-Programmierung noch in den Kinderschuhen steckt. Alle Programme werden aktuell noch in einer Art „Maschinencode für Quantencomputer“ geschrieben und sind entsprechend schwer zu entziffern. In den kommenden Jahren und Jahrzehnten wird sich die Quanten-Programmierung also auch in dieser Hinsicht weiterentwickeln müssen. Die Softwareentwicklung für herkömmliche Digitalcomputer hat es uns vorgemacht. So sind im Laufe der Zeit immer intuitivere Programmiersprachen entstanden, die den eigentlichen Maschinencode immer besser abstrahieren.

Finde das Pik As! Ein Quanten-Algorithmus einfach erklärt

Um Ihnen einen Eindruck von der Andersartigkeit der Quanten-Algorithmen zu vermitteln, versuchen wir mal folgendes Problem zu lösen:

Jemand mischt für uns ein Kartenspiel mit 52 Karten gut durch und breitet die 52 Karten wahllos und verdeckt vor uns aus. Jetzt schreibt er auf jede Kartenrückseite eine Nummer, die „Adresse“. Die Aufgabe soll heißen: Finde die Karte, also die Adressnummer, mit dem Pik As!

Mit unsere Alltagslogik und für jeden herkömmlichen Computer ist der beste Algorithmus für die Lösung sehr einfach und offensichtlich:

• • • Schritt 1: Nimm irgendeine Karte
    • Schritt 2: Drehe sie um und prüfe: Ist es das Pik As?

• • • • • Falls ja: Fertig!
        • Falls nein: Lege die Karte zur Seite und beginne wieder bei Schritt 1.

Im Schnitt brauchen wir für die Lösung ½ * 52 = 26 Durchläufe. Kein einzelner Mensch und kein einzelner Prozessor-Kern könnte jemals diese Aufgabe schneller durchführen. Punkt!

Der Prozessor eines Quantencomputers kann dies sehr wohl. Für ihn sieht die Lösung komplett anders und bizarr aus. Wegen des Quantenparallelismus kann sich der Quantencomputer alle Karten gleichzeitig ansehen und sie prüfen. Er kann sich die gesuchte Karte, bzw. genauer die Adressnummer zu dieser Karte, aber leider nicht so einfach herausfischen. Stattdessen muss er die falschen Karten nach und nach „ausblenden“ und das Pik As nach und nach weiter „einblenden“. Am Ende bleibt dann nur noch das Pik As mit der gesuchten Adressnummer übrig.

Der Algorithmus hierfür ist der berühmte Grover-Algorithmus. Ich stelle ihn in meinem Artikel „Der Grover-Algorithmus und die Suche nach dem Heiligen Gral“ im Detail vor. Dabei werden Sie auch erkennen wie ungemein wichtig und tiefgreifend diese auf den ersten Blick banale Fragestellung ist. Leicht abgewandelt könnte die Aufgabe etwa auch heißen: „Finde die kürzeste Route von allen möglichen Routen“ oder sogar „Finde den Beweis für … (ein wichtiges mathematisches Problem)“.

Für unser Kartenbeispiel funktioniert der Grover-Algorithmus wie folgt:

In unserem Quantencomputer haben wir zunächst jeder Karte ein Bitmuster zugeordnet. Wir suchen letztendlich also das Bitmuster für das Pik As. Jemand anderes hat diese Bitmuster jetzt in den Qubit-Registern unseres Quantencomputers „versteckt“. Wir wissen nicht wo und bekommen stattdessen nur irgendwelche Adressnummern zu den jeweiligen Registern. Diese Adressennummern sind natürlich wieder Qubits.

• • Schritt 1: Zunächst überführen wir die Qubits aller Adressnummern in einen gleichmäßig überlagerten Quantenzustand.

• • Schritt 2: Danach laden wir die unbekannten Bit-Muster der Karten nach und „heften“ sie an ihre jeweiligen Adressnummern (diese Operation nennt man auch „Quantum RAM“).

• • • • Wir haben jetzt einen einzelnen Zustand an dem alle Karten inklusive deren Adressnummern gleich beteiligt sind (die Qubits der Adressen und die Qubits der Bit-Muster sind darin maximal miteinander verschränkt).

• • • • Diesen Zustand können Sie sich als einen einzelnen Zeiger in einem riesigen, abstrakten Raum mit 52 Dimensionen bzw. Richtungsachsen „vorstellen“. Wobei: versuchen Sie es gar nicht erst. Mehr als drei Dimensionen können wir uns sowieso nicht vorstellen: oben/unten, links/recht, vorne/hinten.

• • • • Jede der 52 Richtungsachsen entspricht einer bestimmten Karte. Das gesuchtes Pik As ist eine dieser Achsen. Unser überlagerter Zustand zeigt vollkommen schräg in diesen Raum hinein und ein bisschen in jede der 52 Richtungen.

• • Schritt 3: Der Quantencomputer prüft jetzt in welcher Richtung das Pik As liegt.

• • • • Diese Prüfung ist im Prinzip ein einfaches Unterprogramm, man nennt sie trotzdem etwas geheimnisvoll: Das „Orakel“. Bildlich gesprochen dreht der Quantencomputer den Zeiger mithilfe des Orakels in die Pik As – Richtung.

• • • • Er kann ihn aber leider nur um in einen kleinen Winkel drehen. Dieser Winkel ist umso kleiner, je mehr Karten geprüft werden müssen.

• • • • Der Zeiger ist nach der Prüfung keine gleichmäßige Überlagerung mehr. Er zeigt jetzt etwas mehr in die Pik As – Richtung als in die Richtungen der anderen Karten.

• • Schritt 4: Schritt 3 müssen wir jetzt mehrmals hintereinander ausführen. Der Wissenschaftler Lov Grover hat 1996 nachgewiesen, dass der Zeiger nach √52 ≈ 7.2 Prüfungen in die Richtung des Pik As gedreht wurde. Nach 7 Prüfungen messen wir also die Qubits aus und erhalten die Bit-Darstellung des Pik As und deren Adressnummer.

Folgendes Beispiel zeigt den Grover-Algorithmus für zwei Qubits.

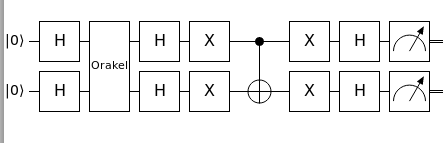
Quantenkomplexität einfach erklärt

Vor einem halbem Jahrhundert begannen Computerwissenschaflter damit, Probleme in Klassen zu unterteilen, je nachdem wie schwierig es ist eine Lösung zu finden. Die Probleme, die relativ effektiv mit einem herkömmlichen Computer gelöst werden können, nannten sie P-Probleme.

Als die ersten Konzepte für Quantencomputer erarbeitet wurden, fügte man die Problem-Klasse BQP hinzu. Dies sind die Probleme, die relativ effektiv mit einem Quantencomputer gelöst werden können.

Mittlerweile weiss man, dass es einen grundlegenden Unterschied zwischen diesen beiden Klassen gibt. Ein Quantencomputer ist prinzipiell in der Lage wesentlich mehr Probleme effektiv zu lösen als ein herkömmlicher Computer. Ein Beispiel hierfür ist die Zerlegung in Primzahlen mit dem Shor-Algorithmus.

Dass aber selbst ein Quantencomputer seine Grenzen hat, wird im folgenden Diagramm deutlich. Es zeigt den Zusammenhang der wichtigen Problem-Klassen, den die meisten Computerwissenschaflter aktuell vermuten (mehr über die dargestellten Klassen erfahren Sie u.a. in meinem Artikel zum Grover-Algorithmus):

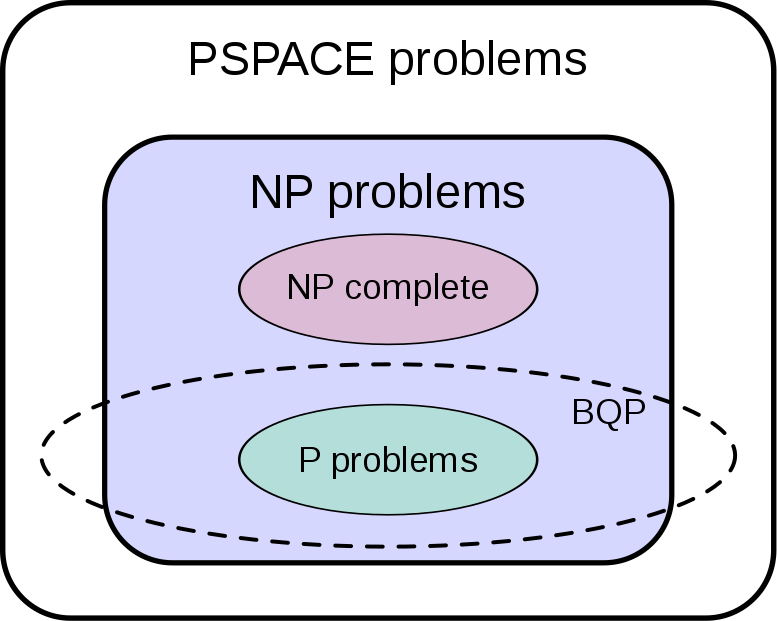
(Quelle: https://en.wikipedia.org/wiki/File:BQP_complexity_class_diagram.svg)

Letzte Änderungen

„quantencomputer-info.de“ ist ein lebendiges Online-Buch, das ich immer wieder aktualisiere und verbesser. Falls Sie ein wiederkehrender Besucher sind, können Sie in den Abschnitten „Letzte Änderungen“ erkennen, was sich seit Ihrem letzten Besuch verändert hat:

• • 07.11.2019:
    • Abschnitt „Die Qubits einfach erklärt“: 2-Qubit-Skizze hinzugefügt
    • Abschnitt „Einsteins spukhafte Verschränkung“: Beispiel und Skizze von 2 verschränkten Qubits hinzugefügt
    • Abschnitt „Quantengatter einfach erklärt“: Ein paar Erläuterungen über „Quirk“ hinzugefügt
    • Abschnitt „Finde das Pik As!“: QRAM-Funktionalität hinzugefügt
    • Abschnitt „Letzte Änderungen“ hinzugefügt
  • 04.07.2019:
    • Abschnitte „Finde das Pik-As“ und „Quantenkomplexität einfach erklärt“ hinzugefügt“

Fußnoten