Im Folgenden geben ich Ihnen einen detaillierten Überblick, welche Quantencomputer-Angebote bereits heute schon existieren und welche konkreten Pläne die Industrie für die Zukunft verfolgt. Dabei erhalten Sie einen Einblick darüber, was ein Quantencomputer ist und wie man ihn verwenden kann. Diesen Artikel aktualisiere ich regelmäßig und halte Sie über die aktuellen Entwicklungen in der Quantencomputer-Industrie auf dem Laufenden.

Ein Quantencomputer von IBM (Quelle IBM Research)
Als ich 2018 den vorliegenden Artikel zum ersten Mal verfasst habe, war die Situation der kommerziellen Hardware-Hersteller von Quantencomputern und deren Architektur-Strategien ziemlich übersichtlich. Nachdem ich ihn in der Zwischenzeit ein paar Mal angepasst habe, stelle ich fast drei Jahre später fest, dass ich den Text in großen Teilen neu schreiben sollte. Zwar haben sich die Keyplayer von vor drei Jahren weiter etabliert und beeindruckende Ergebnisse vorzuweisen. Aber weitere Firmen sind seitdem auf der Bühne erschienen, die den Markt auf gemischt haben. Gleiches gilt für die Architektur-Strategien: Hatte es 2018 noch den Anschein, als ob es auf absehbare Zeit keine andere ernstzunehmende Quantencomputer-Technologie außer den supraleitenden Qubits geben würde, so war das Jahr 2020 wohl das Jahr der Ionenfallen-Quantencomputer. Der Jahresabschluss aber gehörte den photonischen Quantencomputern, die immer mehr an Fahrt aufnehmen und deren Hersteller gerade spielend Investorengelder einsammeln. Vermutlich wird sich dieser Trend der Diversifizierung in Zukunft weiter fortsetzen.
Im Folgenden stelle ich Ihnen die Hersteller, deren Architekturen und Visionen sehr detailliert vor. In zahlreichen Fußnoten erfahren Sie zusätzliche Hintergründe und erhalten Verweise auf vertiefende Texte und Originalarbeiten. Der Artikel richtet sich an Einsteiger, die einen wirklich umfassenden Überblick erhalten wollen. Er richtet sich allerdings auch an Fortgeschrittene, die auf der Suche nach dem ein oder anderen neuen, spannenden Detail sind.
Was ist ein Quantencomputer?
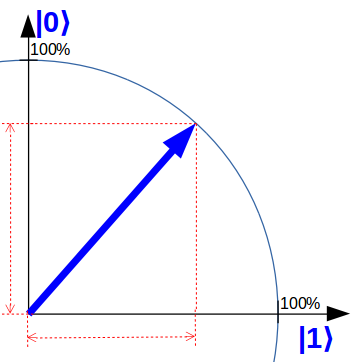
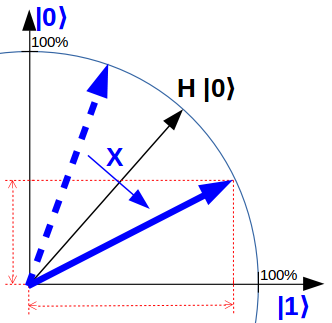
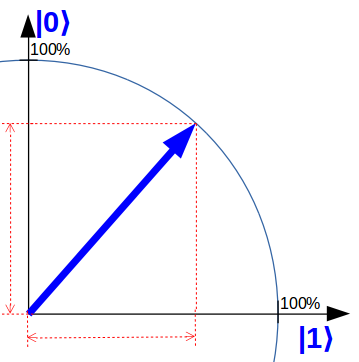
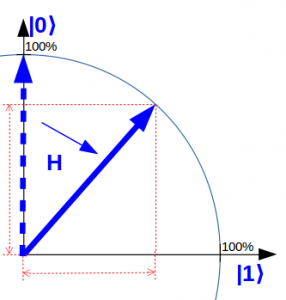
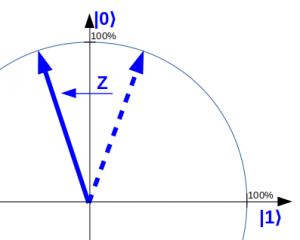
Ein Quantencomputer ist eine Rechenmaschine, die nicht mit unserer Alltagslogik arbeitet, sondern mit der Quanten-Logik. Die elementaren Recheneinheiten sind dabei Quantenbits („Qubits“). Anders als herkömmliche Bits können Qubits beliebige Überlagerungen von den Zuständen „0“ und „1“ annehmen. Dies ist eine der grundlegenden Eigenschaften der Quantenmechanik („Welle-Teilchen-Dualismus“ genannt). Ich verwende dafür auf quantencomputer-info.de eine vereinfachte Qubit-Darstellung, die das Wesentliche aber gut wiedergibt i. Ein herkömmlicher Computer verwendet zur elektronischen Schaltung elementarer Logikbausteine sogenannte Gatter, die auf unserer Alltagslogik basieren. Also z.B. NICHT-, UND- und ODER-Gatter. Ein universeller Quantencomputer verwendet stattdessen Quantengatter, welche die Quantenlogik abbilden. Diese heißen z.B. H, X, Y, Z, CNOT.
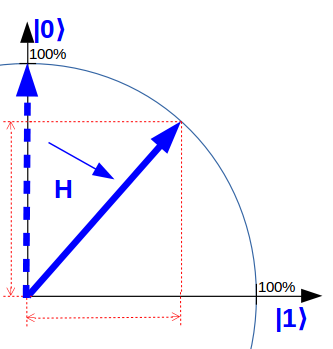
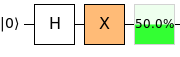
Vereinfachte Darstellung eines Qubits, auf das ein H-Quantengatter ausgeführt wird und damit zu einer gleichmäßigen Überlagerung von „0“ und „1“ wird
Anders als herkömmliche Computer verdoppelt ein Quantencomputer sein Leistungspotential mit jedem zusätzlichen Qubit (also eine explosionsartige bzw. exponentielle Steigerung). Aktuelle Quantencomputer sind noch klein, mit aktuell 10 bis 65 Qubits, und stark limitiert (NISQ = „noisy intermediate scale quantum“, mehr dazu weiter unten im Text). Ein Quantencomputer mit einer Größe von etwa 26 perfekten Qubits lässt sich noch mit einem normalen Laptop „simulieren“ ii. Die Luft für herkömmliche Computer wird dann aber wegen der erwähnten Steigerungsrate ganz schnell dünner: Ab einer Größenordnung von etwa 50 Qubits lässt sich ein Quantencomputer von keinem aktuellen Supercomputer mehr simulieren (mehr dazu im Absatz zu Googles Quantencomputer) und danach werden die Unterschiede gewaltig iii. Aufgrund seiner andersartigen Logik, lassen sich herkömmliche Programme allerdings nicht auf einen Quantencomputer übertragen, sondern man benötigt hierfür ganz neue Quanten-Algorithmen, die Gegenstand intensiver Forschung sind. Für einige wichtige Anwendungsfälle wurden bereits Algorithmen gefunden, die einen gewaltigen Geschwindigkeitsvorteil gegenüber herkömmlichen Methoden besitzen (z.B. der „Shor-Algorithmus“ für die Primfaktorzerlegung). Diese eint allerdings auch die Tatsache, dass sie sehr große, fehlerkorrigierende Quantencomputer benötigen.
Für weitere Informationen empfehle Ihnen meine umfangreiche Einführung „Der unglaubliche Quantencomputer einfach erklärt“. Dort werden Sie noch mehr spannende Dinge über das Prinzip der Quantencomputer erfahren. Unter anderem erkläre ich Ihnen anhand eines Zeigerbildes wie die „spukhafte“ Quanten-Verschränkung funktioniert. Außerdem erfahren Sie wie ein Quantencomputer-Programm aussieht und wie Sie eines schnell mal selbst online ausprobieren können. Zusätzlich erkläre ich Ihnen auf einfache Weise und sehr bildlich, wie ein bekannter Such-Algorithmus für Quantencomputer (der „Grover-Algorithmus“) in etwa funktioniert.
Qubitzahl, Quantenvolumen und Fehlerraten: Die „bittere Wahrheit“ über NISQ-Quantencomputer

Techniker von IBM am „dilution refrigerator“ eines NISQ-Quantencomputers (Quelle IBM Research)
Um das Potential von konkreten Quantencomputern zu Klassifizieren, verwendete man bis vor Kurzem in erster Linie die Anzahl von Qubits. Hierbei liegen supraleitende Quantencomputer aktuell deutlich vorn. Die Kennzahl ist durchaus sinnvoll, da ein Quantencomputer mit jedem zusätzlichen Qubit seine Leistungsstärke verdoppelt. Zumindest auf dem Papier, denn die aktuellen NISQ-Quantencomputer besitzen diverse entscheidende Einschränkungen:
Aufgrund von Umgebungsstörungen können sie den Quantenzustand der Qubits meistens nur für eine kurze Zeitspanne aufrechterhalten (ausgedrückt über die „T1-“ und „T2-Decoherence-Time“). Unter anderem hierbei unterscheiden sich die Ansätze der Quantencomputer-Anbieter stark: Ionenfallen-Quantencomputer besitzen z.B. eine wesentlich größere Qubit-Güte (Sekunden bis zu Stunden) als supraleitende Qubits (etwa 100 Mikrosekunden) iv.
Jede Einzelschaltung hat eine gewisse Fehlerrate („Gate-Fidelity“). Diese sind um viele Größenordnungen größer als bei herkömmlichen Computern und sind der Hauptgrund, warum Quantenprogramme aktuell bestenfalls zweistellige Schaltungstiefen besitzen dürfen: Aktuelle Fehlerraten sind für 1-Qubit-Gatter Größenordnungen von: 0.1% bzw. 1 Fehler je 1000te Schaltung und für 2-Qubit-Gatter 1% bzw. 1:100.
Nicht alle Qubits können paarweise miteinander verschaltet werden („Connectivity“). Für supraleitende Quantencomputer können normalerweise nur die nächsten Nachbar-Qubits kombiniert werden. Das bedingt dann zusätzliche, fehlerbehaftete Tauschoperationen („Swaps“). Auch hierbei sind Ionen-Fallen Quantencomputer wesentlich flexibler.
Im Verbund können sich die Qubits und Quanten-Schaltungen gegenseitig stören („Crosstalk“).
Beim Initialisieren der Qubits und beim Auslesen des Ergebnisses können zusätzliche Fehler auftreten („Readout Error“ bzw. „SPAM-Error“, Größenordnung 1% bzw. 1:100).
Was diese Fehlerquellen und Einschränkungen in der Praxis bedeuten, können Sie z.B. sehr schön in der Untersuchung „The Bitter Truth About Quantum Algorithms in the NISQ Era“ von der Universität Stuttgart erkennen v. Ob man in der Lage sein wird mit NISQ-Quantencomputern einen Quantenvorteil in praktischen und Industrie-relevanten Anwendungen zu erzielen ist aktuell noch offen und Gegenstand intensiver Forschung vi. Auf der anderen Seite steigt die Zahl der Firmen in etablierten Märkten, die bereits in den nächsten Jahren Budget für das Quantencomputing einplanen, stark an vii.
Um den Einschränkungen von NISQ-Quantencomputern in einer einzigen Kennzahl Rechnung zu tragen hat IBMs Quantum-Team 2018 ein Protokoll entwickelt, dass die „effektive“ Qubitanzahl ermitteln soll. Die Kennzahl „Quantenvolumen“ („Quantum Volume“) basiert auf einem Benchmark-Protokoll viii: Dafür misst man das größtmögliche „quadratische“ Quantenprogramm eines bestimmten, einigermaßen aussagekräftigen Typs, das „überzeugende“ Ergebnisse liefert („quadratisch“ bedeutet hier: Die Anzahl der verwendeten Qubits und die Schaltungstiefe sollen gleich sein). Die Quantenprogramme für die Benchmarks müssen einen bestimmten, zufallsbasierten Aufbau besitzen und prüfen dabei die obengenannten Einschränkungen. Allerdings darf der Quantencomputer diesen Aufbau für praktische Gründe zunächst in eine hardware- freundlicheren Aufbau umkompilieren. Aus diesem Quadrat ermittelt man eine effektive Qubitanzahl „q“ (die Firma IonQ nennt diese Zahl auch „algorithmische Qubits“). Das Quantenvolumen ist dann der Wert 2 hoch „q“, um den exponentiellen Charakter der Quantencomputer Rechnung zu tragen.
Die Kennzahl „Quantenvolumen“ hat sich mittlerweile größtenteils industrieweit etabliert. Sie ist aber nicht frei von Kritik. Scott Aaronson, einer der renommiertesten Forscher für Quantencomputing, empfiehlt eher auf alle oben genannten Kennzahlen zu achten ix, weil die Differenzierungen von Fall zu Fall gewaltige Auswirkungen haben können. Ein normaler Laptop-Rechner hätte z.B ein viel größeres Quantenvolumen als der Quantencomputer Sycamore in Googles Quanten-Überlegenheits-Nachweis (hierzu später mehr). Im Umkehrschluss bedeutet Aaronsons Kritik: Gerade in der NISQ-Ära kann die Wahl der Hardware für einen bestimmten Algorithmus und eventuell für einen bestimmten Anwendungsfall entscheidend sein.
Googles supraleitender Quantencomputer „Sycamore“ und die „Quanten-Überlegenheit“

(Google Campus, Quelle „Niharb“)
2013 gründete Google das Quantum AI Lab. Das Quantum AI Lab ist ein Team, das von dem langjährigen, deutschen Google-Mitarbeiter und KI-Forscher Hartmut Neven geführt wird. Es sollte zunächst die Möglichkeiten untersuchen, eine völlig neue Quanten-Hardware der Firma D-Wave-Systems für die künstliche Intelligenz zu nutzen x. Mehr zu D-Waves „Quanten-Annealer“ weiter unten im Text. Als sich abzeichnete, dass der Quantencomputer von D-Wave noch gewisse Einschränkungen hatte, beschloss Google einen eigenen, universellen Quantencomputer zu bauen. 2014 startete das Google Quantum AI Lab eine Koorperation mit dem bekannten Physiker John Martinis von der University of California, Santa Barbara. Er ist einer der führenden Experten für supraleitende Qubits und sollte den Bau des Quantencomputers leiten.
Die Supraleiter-Technologie (bzw. genauer „Circuit QED“) ist einer der aussichtsreichsten Kandidaten um verlässliche, universelle Quantencomputer zu bauen xi xii. Diese gründet letztendlich auf integrierten Schaltkreisen, die durch bekannte Fertigungsmethoden auf einen herkömmlichen Chip gedruckt werden können. Die Schaltkreise verhalten sich ähnlich wie normale Schwingschaltkreise und werden enorm heruntergekühlt, bis fast zum absoluten Temperatur-Nullpunkt („Cryogenics“). Das entstandene Elektronenkondensat erhält dadurch supraleitende Quanteneigenschaften. In dem man gezielt Lücken in jeden Schaltkreis einbaut, sogenannte „Josephson Junctions“, ist es möglich die ansonsten beliebig vielen Zustände des Quantenschaltkreises zu einem Quantensystem mit zwei isolierten Zuständen zu reduzieren xiii („0“ und „1“): Ein supraleitendes Qubit ist entstanden.
Durch schlangenförmige Wellenleiter, sogenannte „waveguide resonators“ die sich ebenfalls auf dem Chip befinden, werden die Supraleiter-Qubits mit einzelnen Lichtteilchen bzw. Photonen im Mikrowellen-Bereich bestrahlt. Die Qubits führen dudurch feinjustierte Übergänge zwischen den beiden Zuständen „0“ und „1“ aus („Rabi-Oszillationen“). Auf diese Weise können die Quantengatter geschaltet und somit die Qubits im Laufe eines Quantenprogramms geändert werden (z.B. die Gatter H, X, Y, Z und CNOT). Auf ähnliche Weise werden die Qubits am Ende des Programms ausgelesen: Die unterschiedlichen Zustände der Qubits verschieben die Resonanzfrequenz der schlangenförmigen Wellenleiter, und diese Verschiebung kann gemessen werden xiv. Der winzig kleine Quantenchip wird an den Fuß eines Gerüsts eingehangen, das aus thermischen Leitern und Kühlaggregaten besteht, die den Chip herunterkühlen („dilution refrigerator“). Die Verbindungen bestehen z.B. aus gebogenem Gold, welches ein idealer thermischer Leiter ist und fexibel auf Verformungen reagiert. Außerdem sieht es ziemlich cool aus :-)! Der ganze Aufbau wird oben mit der externen Steuerelektronik verkabelt und schließlich in einen großen Vakuum-Behälter platziert, der außerdem das Erdmangetfeld abschirmen muss.
Der Vorteil der Supraleiter-Technologie ist es, dass die einzelnen Bestandteile groß im Vergleich zu anderen Quantenobjekten sind. Dadurch lassen sie sich vergleichsweise einfach herstellen und verschalten und ermöglichen verschiedene Architekturansätze (in Googles und IBMs Fall sind es z.B. sogenannte „Transmon“-Qubits). Die Nachteile sind die relativ kurze Lebensdauern der Qubit-Zustände und die benötigte Tiefkühltechnik.

Nahaufnahme eines Quantenchips mit 4 supraleitenden Qubits, allerdings von Googles Konkurrenten IBM, Quelle IBM / Wikipedia: Die schlangenförmigen Linien sind die oben erwähnten Wellenleiter für Mikrowellen-Photonen. Die eigentlichen Qubits sind die kleinen Köpfe der „Nägel“, die nach außen zeigen. Den entsprechenden Fachartikel in „Nature“ 2017 finden Sie ebenfalls über den Link
Googles Labor sammelte zunächst unter John Martinis Leitung eine Zeit lang Erfahrungen mit einem 9-Qubit-Quantencomputer. Später begannen sie die Technologie hochzuskalieren. Ziel dabei war es auch das prestigeträchtige Ziel der „Quanten-Überlegenheit“ als erste Gruppe zu erreichen. Anfang 2018 gab Googles Team bekannt, dass ein 72-Qubit-Quantencomputer im Testbetrieb sei, und es sah alles nach einer gewaltigen Sensation aus. Tatsächlich wurde der Quantencomputer „Bristlecone“ allerdings nie in Betrieb genommen. Diese Episode ist ein Beispiel dafür, dass die reine Qubit-Anzahl zunächst nichts aussagt, wenn die anderen relevanten Kennzahlen nicht in den Griff bekommen werden. Außerdem zeigt sie sehr anschaulich, dass alle Ankündigungen der Quantencomputer-Hersteller eine gewisse Unsicherheit besitzen und jeder Schritt mit neuen, zum Teil großen, technologischen Hürden verbunden ist.
Im September 2019 sorgte Google dann aber durch eine geleakte Vorveröffentlichung für einen Paukenschlag. Darin wurde der neue und bis dato unbekannte Quantencomputer „Sycamore“ mit einer Größe von 53 Qubits beschrieben. Zum Vergleich: Der zu diesem Zeitpunkt größte Quantencomputer von IBM besaß 30 Qubits. Google war in der Lage auf „Sycamore“ eine spezielle Quanten-Rechenaufgabe (das „Quantum Random Circuit Sampling“) in Sekundenschnelle auszuführen, die auf den schnellsten aktuellen Supercomputern vermutlich 10 000 Jahre dauern würde. Die offizielle Veröffentlichung folgte einen Monat später. Die Rechenaufgabe war zwar zunächst rein akademisch. Googles Weckruf beweist aber, dass das Prinzip der Quantencomputer und die Vorhersagen dafür tatsächlich in der Praxis umgesetzt werden können: Für gewisse Probleme funktionieren Quantencomputer grandios besser als herkömmliche Computer. Möglich wurde der Durchbruch auch dadurch, dass Martinis Team es schaffte die Fehlerraten der Quantengatter um einen Faktor 10 zu unterdrücken und zwar unabhängig davon wie viele Schaltungen gerade aktiv waren. Alle Details und Erläuterungen zu diesem großen Meilenstein erfahren Sie in meinem Artikel „Googles Nachweis der Quanten-Überlegenheit“.
Im Anschluss an Googles Arbeit gab es ein paar Veröffentlichungen, die das Ergebnis in Teilen relativierten (u.a. von IBMs-Team). Die Kernaussage hat aber bis heute bestand. Interessanterweise tauschte Googles Team ein Jahr später die Rollen und stellte seinerseits die Ergebnisse des chinesischen Teams in Teilen in Frage (s.u.den Abschnitt über Chinas Quantencomputer).
Einige Wochen später besuchte John Martinis das California Institute of Technology (Caltech) und hielt dort einen ersten Vortrag zu dem Durchbruch xv. Hier bekommen Sie viele spannenden Details über Googles Quantencomputer zu hören … mit den Worten des Meisters :-).
Nebenbei ist Sycamore aktuell auch der erste Quantencomputer der eine planare, schachbrettartige Anordnung der Qubits mit einer Kopplung der nächsten Nachbar-Qubits besitzt. Diese Qubit-Anordnung ist zum Hochskalieren zukünftiger Quantencomputer besonders wichtig. Um die NISQ-Ära hinter sich zu lassen und wirklich komplexe Quantenprogramme auszuführen, müssen Quantencomputer „fehlerkorrigierte“ Qubits besitzen. Aus diesem Grund ist die „Quantenfehlerkorrektur“ seit jeher ein wichtiger Forschungszweig auf dem Gebiet. Hierbei werden verschaltete Qubitgruppen zu einem einzigen „logischen Qubit“ zusammengefasst, das dann korrigiert werden kann. Die Kehrseite dabei ist, dass dies die tatsächliche Anzahl von verfügbaren Qubits teils drastisch reduziert. Der aussichtsreichste Algorithmus zur Quantenfehlerkorrektur ist der sogenannte „Surface Code“ xvi, der gerade diese planare Qubit-Anordnung benötigt.
Googles Team und die Roadmap
Kurz nach Googles Veröffentlichung endete die erfolgreiche Koorperation zwischen Google und Martinis ziemlich überraschend xvii. Mittlerweile ist Googles Hardware-Team aber wohl so stark aufgestellt, dass es den vorgezeichneten Weg weiter beschreitenwird.
Im Herbst 2020 veröffentlichte Hartmut Neven Googles Roadmap für die nächsten 10 Jahre xviii. Darin skizziert er, wie sein Hardware-Team die aktuelle Technologie bis zum Jahr 2029 zu einem Quantencomputer mit 1000 logischen, fehlerkorrigierten Qubits hochskalieren will. Dabei plant Googles Hardware-Team zunächst zu verifizieren, ob der Surface-Code, die Quantenfehlerkorrektur und logische Quantengatter in der Praxis überhaupt umgesetzt werden können xix.
Neben der Weiterentwicklung der eigenen Hardware, untersucht Googles Quantum AI Lab die Anwendungsmöglichkeiten von heutigen und von zukünftigen Quantencomputern und zwar besonders in den Bereichen Maschinelles Lernen, Chemische Simulationen und Optimierungsaufgaben xx xxi. Dazu ist das Team mit einigen Spitzenforschern stark besetzt. Die Algorithmen für NISQ-Quantencomputer teilen die Eigenschaft, dass sie Quanten-klassische „Hybrid-Algorithmen“ sind. Dazu werden Quantenschaltkreise konstruiert, ausgemessen und dann mittels herkömmlichen Computern für den nächsten Durchlauf optimiert. Dadurch werden schrittweise die Stärken von sowohl Quantencomputern als auch von klassischen Computern ausgenutzt. Diese Verfahren haben den bestechenden Vorteil, dass ihr Quantenanteil sehr kurz sein kann und noch von den aktuellen Quantencomputern bewältigt werden kann. Mehr dazu erfahren Sie auch in meinem Artikel „Anwendungen für Quantencomputer“.
Für die eigenen Quantenprogramme hat Google mit „Cirq“ eine Erweiterung für die beliebte Programmiersprache Python veröffentlicht xxii, über die Quantencomputer ferngesteuert werden können. Basierend auf „Cirq“ hat das Quantum AI-Team die Entwicklung weiterer OpenSource-Frameworks für die chemische Simulation xxiii und für Maschinenlernen bzw. künstliche Intelligenz xxivgestartet.
Das Quantum AI-Team sucht aktuell gezielt nach Kooperationspartner mit einer starken Forschungsabteilung, um die Möglichkeiten der eigenen Hardware für diese Anwendungsgebiete gezielt an konkreten Beispielen zu untersuchen. Googles Quantencomputer stehen aktuell nur diesem exklusiven Anwenderkreis zur Verfügung. Ganz im Gegensatz zu dem anderen Big Player für supraleitende Quantencomputer ….
IBMs Quantencomputer-Flotte in der Cloud

Ein Quantencomputer von IBM (Quelle IBM Research)
IBM ist der Tech-Riese, der von Anfang stark im Bereich Quantencomputer engagiert war. Bereits 2001 sorgte das Unternehmen für Aufsehen, als es den ersten experimentellen Beweis für Shor‘s berühmten Faktorierungsalgorithmus für Quantencomputer lieferte xxv.
Im Mai 2016 startete IBM dann ein völlig überraschendes und sensationelles Cloud-Angebot: In der „IBM Quantum Experience“ stellte IBM als erstes Unternehmen überhaupt den eigenen 5 Qubit Quantencomputer für die Öffentlichkeit zur Verfügung. Seitdem hat IBM insgesamt 28 Systeme zum Einsatz gebracht. Dabei stehen mehrere Quantencomputer mit bis zu 32 Qubits für jeden Interessenten zur Verfügung. Die größeren Systeme sind für Premium-Kunden vorbehalten. Aber selbst die „kleineren“ Quantencomputer werden regelmäßig verbessert und ihr Quantenvolumen wird vergrößert. IBMs aktuell leistungsstärkster Quantencomputer ist der „Hummingbird“ mit 64 Qubits.
https://www.ibm.com/quantum-computing/experience/
Die Quantum Experience von IBM ist über die Jahre zu einer beeindruckenden Größe herangewachsen: Aktuell betreibt IBM insgesamt 18 Quantencomputer gleichzeitig, die für 250 000 User verfügbar sind (Stand Februar 2021). IBMs Cloud-Angebot hat bisher 500 Milliarden Quantenprogramme ausgeführt (mit Tageshöchstwerten von 1 Milliarde Quantenprogrammen), was unter anderem zu 400 wissenschaftlichen Veröffentlichungen führte xxvi.
Wie Googles Quantencomputer sind IBMs Systeme universelle Quantencomputer und basieren ebenfalls auf der Supraleitertechnologie. Dabei werden die üblichen Standard-Quantengatter durch native Quantengatter erzeugt, die charakteristisch für die konkrete Hardware sind. Ein X-Gatter wird z.B. bei IBM durch ein Quantengatter mit der Bezeichnung „U3(π,0,π)“ erzeugt. Die Umwandlung in die nativen Quantengatter bezeichnet man als Transpilation. An dieser Parametrisierung erkennt man auch, dass die Effektivität von gewissen Schaltungskombinationen von Quantencomputer zu Quantencomputer stark abweichen kann.
Wie für alle Quantencomputer gilt auch für die Systeme von IBM: Qubit ist nicht gleich Qubit. Jedes Qubit besitzt seine eigene charakteristische Decoherence-Time (s.o.) und nicht jedes Qubit kann mit jedem anderen Qubit verschaltet werden. IBM muss die Qubits in seinen Quantencomputern deshalb ständig neu kalibrieren. Die aktuellen Metriken und die Auslastung der einzelnen Systeme können die Anwender jederzeit einsehen und eine konkrete Implementierung sollte die aktuellen Metriken berücksichtigen und dafür optimiert werden.
Als Programmierschnittstelle für Anwender stellte IBM im Jahr 2016 zunächst einen grafischen „Composer“ bereit, über den einfache Schaltkreise für die Quantencomputer schnell zusammen geklickt werden können.
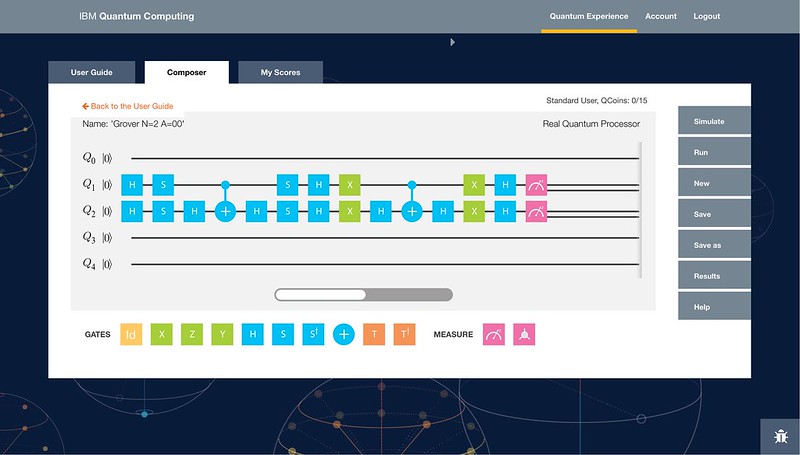
IBMs Composer für Quantenprogramme (Quelle IBM Research)
Kurze Zeit später veröffentliche IBM die Erweiterung „Qiskit“ für die beliebte Programmiersprache Python. Über Qiskit können Anwender Quanten-Programme zunächst lokal auf dem eigenen Rechner in einem Simulator vorbereiten und dann an den gewünschten Quantencomputer in der Quantum Experience schicken.
Aufgrund der riesigen Anwenderbasis von IBMs Cloudangebot ist „Qiskit“ derzeit das mit Abstand beliebteste Framework für Quantenprogramme. IBM entwickelt hierfür regelmäßig neue Module: Mit „Pulse“ veröffentlichte IBM z.B. vor Kurzem ein Modul, mit dem der Anwender die nativen Quantengatter der Systeme direkt ansprechen kann. Normalerweise erledigt das Transpilation das Framework komplett selbstständig. Ebenfalls relativ neu ist das Modul „Gradient“ mit dem die sehr komplexen Optimierungsoperationen der oben erwähnten „Hybrid-Algorithmen“ für klassische Rechner und Quantenrechner gezielt unterstützt werden. Neben dem Framework selbst enthält Qiskit eine Vielzahl von Beispielprogrammen und zwar auch zu aktuellen, wissenschaftlichen Veröffentlichungen. IBM veranstaltet regelmäßige „Qiskit Camps“ xxvii und Qiskit-Hackathons. Auf Slack.com gibt es einen eigenen Qiskit-Channel, in dem aktuell etwa 15 000 Mitglieder zusammenarbeiten.
In meinem Artikel „Quantencomputer programmieren mit IBMs Qiskit“ erfahrend sie noch mehr über das Programmieren mit Qiskit. Insbesondere zeige ich Ihnen dort, wie man den sogenannten „Grover-Algorithmus“ konkrekt programmiert.
Auf der Quantum Experience finden sich außerdem eine Vielzahl von sehr hilfreichen Dokumentationen: Der „Userguide“ vermittelt Einsteigern auf möglichst einfache Weise einen Überblick über das Quantencomputing und erläutert das Prinzip von ein paar grundlegenden Quanten-Algorithmen xxviii. Das „Textbook“ ist ein Lehrbuch in Form von „Jupyter Notebook“-Seiten und eine konkrete Einführung in das Quantencomputing mit Qiskit xxix. Wie Qiskit selbst ist das „Textbook“ auf Github als Opensource-Projekt öffentlich zugänglich.
IBMs Roadmap
Im September 2020 kündigte IBM eine Roadmap für die nächsten Jahre an. Im Gegensatz zu Google gab das IBMs Team dabei ein paar konkretere Details bekannt xxx. Demnach soll bereits im Jahr 2021 ein 127-Qubit Quantencomputer mit dem Namen „Eagle“ in Betrieb genommen werden. Im Jahr 2022 soll dann ein 433-Qubit- und 2023 sogar ein 1,121-Qubit-System folgen. Falls IBM diesen Fahrplan aufrecht halten kann, wären dies jeweils gewaltige technologische Sprünge. Für die folgenden Schritte muss IBM zunächst eine neue Tiefkühltechnologie einführen, die in der Lage ist, wirklich große Quantencomputer bis fast zum Temperatur-Nullpunkt zu kühlen. Auch an diesem „Goldeneye“-System forscht das Team.
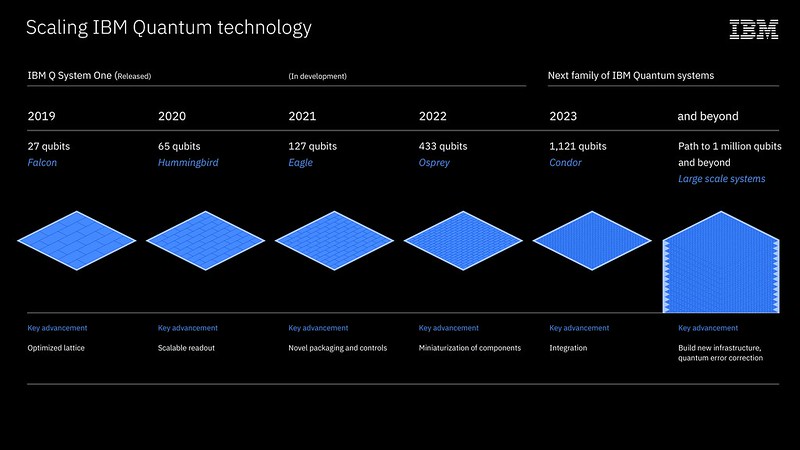
IBM Roadmap für Quantencomputer (Quelle IBM Research)
Wie auch die anderen Hersteller hat IBM dabei aber tatsächlich besonders ein Fernziel im Auge: Die Entwicklung eines hochskalierten Quantencomputer, der in der Lage ist die Algorithmen für die Quantenfehlerkorrektur auszuführen. Dies reduziert zwar die effektive Anzahl an „logischen Qubits“ um etwa den Faktor 1000, dafür sind dadurch beliebig lange Quantenprogramme möglich. Insbesondere auch die Programme, von denen man jetzt schon weiß, dass sie einen Quantenvorteil gegenüber herkömmlichen Computeralgorithmen besitzen werden.
Für die zukünftige Quantenfehlerkorrektur verfolgt IBM eine Strategie, den das Team als „Bottom-Up“-Ansatz bezeichnet. Hierzu haben die Forscher des Konzerns einen neuen Fehlerkorrektur-Algorithmus entwickelt, der speziell auf genau die Qubit-Struktur optimiert ist, die sie gut kontrollieren können xxxi. In Zukunft verwendet IBM für die eigenen Quantencomputer deshalb nur noch eine sogenannte „heavy-hexagon“-Qubit-Struktur.
Neben diesem Fernziel forscht IBM weiterhin daran, dass Potential der aktuellen NISQ-Quantencomputer auszuloten. Dazu sind am „IBM Quantum Network“ etwa 130 Großkonzerne (wie Daimler, Samsung und JP Morgan), Forschungseinrichtungen und Startups beteiligt, die entsprechende Anwendungen zusammen untersuchen xxxii. Das selbst mit sogenannten „Noisy Shallow Quantum Circuits“ auf NISQ-Systemen ein Quantenvorteil gegenüber herkömmlichen Methoden möglich ist, berechnete das Team 2020 in Zusammenarbeit mit der Technischen Universität München xxxiii.
Rigetti Computing‘s Quantencomputer: Ein David unter Goliaths
In 2013 verließ Chad Rigetti das Quantencomputer-Team bei IBM und gründete die Firma Rigetti Computing. Über mehrere Finanzierungsrunden konnte er genug Investoren für seine Pläne gewinnen: Einem neuen Global Player im Quantencomputer-Markt. Mittlerweile besitzt die Firma ein üppiges Kapitalpolster. Im Juni 2017 startet Rigetti Computing das eigene Quantencomputer-Cloudangebot xxxiv. Aktuell bietet Rigetti fünf Quantencomputer mit bis zu 28 Qubits an. Wie IBM und Google setzt Rigetti dabei auf supraleitende Qubits. Und ebenfalls richtet sich Rigetti als „Fullstack“-Anbieter aus: Also als ein Anbieter der von der Hardware über die Cloudangebote und den Programmierschnittstellen bis hin zu Highlevel-Anwendungen die gesamte Quantencomputer-Palette anbietet. Auch Rigetti setzt als Programmierschnittstelle auf eine Python-API mit dem Namen „Forest“. Als Anwendungsbeispiel für ihr Komplettpaket geben sie etwa die Simulation von Bindungsenergien in Atomenkernen an xxxv.
Quantencomputer durch Ionenfallen
Die Geschichte der Ionenfallen-Quantencomputer („Ion-Trap“) beginnt in Innsbruck, Österreich. Wenige Wochen nachdem Ignacio Cirac and Peter Zoller im Jahr 1995 von Shors spektakulären Faktorierungsalgorithmus hörten, hatten sie die Idee Ionen in sogenannten Ionenfallen mit geeignetem Laserlicht zu bestrahlen, um damit sowohl Qubits als auch die grundlegenden Quantengatter zu erzeugen xxxvi xxxvii xxxviii.
Ionen sind nichts anderes als angeregte bzw. geladene Atome. Für einen Quantencomputer haben sie den riesigen Vorteil, dass sie komplett identische Quantensysteme darstellen. Hinzu kommt, dass z.B. die Hyperfeinstruktur-Zustände von Ionen sehr langlebig sein können (aus diesem Grund werden solche „hyperfine clock states“ auch für Atomuhren verwendet), und sich sehr gut auf ein Zwei-Zustands-System reduzieren lassen: Ein Qubit. Einfangen und kontrollieren lassen sich einzelne Ionen in einer Ionenfalle, für die der deutsche Physiker Wolfgang Paul mit anderen 1989 den Nobelpreis bekam („Paulfalle“) xxxix. Aktuelle Ionenfallen können in Miniaturgröße hergestellt werden und bis zu 50 einzelne Ionen bewältigen. Die hier vorgestellten Ionenfallen-Quantencomputer verwenden alle Yb+ Ionen, da die notwendigen Laser hierfür besonders günstig für den Betrieb sind. Für die Quantengatter induzieren die Laser die Zustandswechsel der einzelnen Qubits (z.B. von Zustand „0“ nach Zustand „1“) nur über Zwischenzustände, die ähnlich wie eine Barriere wirken, und unbeabsichtigte Zustandswechsel unwahrscheinlich machen („stimulierte Raman-Übergänge“). Mit einer ähnliche Methode werden die Qubits für den Start eines Quantenprogramms im Vorfeld in einen definierten „0“-Zustand „gepumpt“, der wie eine Sackgasse keine Übergänge in die Rückrichtung zulässt.
Für die Praxis haben Ionenfallen noch einen weiteren großen Vorteil: Zwar müssen Ionenfallen die Ionen ebenfalls „herunterkühlen“, da diese aber vollkommen isoliert sind, erreichen die Fallen dies über eine Rundumbestrahlung durch Laserlicht. Dies stoppt die Ionen in Richtung der Eigenbewegung immer weiter ab. Dadurch kann ein Ionenfallen-Quantencomputer, ganz im Gegensatz zu einem Supraleiter-Quantencomputer, sogar bei Zimmertemperatur betrieben werden!
Zoller und Cirac haben mittlerweile zusammen mit ihrem Innsbrucker Kollegen Rainer Blatt das Startup „AQT“ gegründet xl. Ihr zunächst theoretischer Ansatz wurde von einem Team um Christopher Monroe (damals am National Institute of Standards and Technology in Colorado) noch im selben im Jahr 1995 experimentell bestätigt xli. Monroe gründete 2015 zusammen mit anderen die Firma „IonQ“.
Neben einigen klaren Vorteilen (z.B. sehr stabile Qubits, volle Qubit-Konnektivität, Betriebstemperatur) besteht bei Ionenfallen-Quantencomputer die große Herausforderung, dass viele Fallen miteinander kombiniert werden müssen, um die Technologie hochzuskalieren.
Honeywell und der erste kommerzielle Ionenfallen-Quantencomputer weltweit

Honeywells Zentrale in New Jersey, Quelle Wikipedia
Einmal im Jahr versammelt sich das Who-Is-Who der Quantencomputer-Branche in der Konferenz „Quantum For Business“ (kurz „Q2B“) der Startup-Firma QCWare aus dem Silicon Valley. Ein Highlight der Q2B 2019 war definitiv der spannende Vortrag von Tony Uttley der Firma Honeywell xlii. In ihm stellt Uttley den ersten kommerziellen Ionenfallen-Quantencomputer weltweit vor. Die Neuigkeit war tatsächlich eine Überraschung gewesen: Obwohl Honeywell in vielen Technologiefeldern stark vertreten ist, hatte man den Konzern beim Thema Quantencomputer eigentlich nicht auf dem Schirm gehabt. So konnte die Firma sein vielfältiges Knowhow in verwandten Technologien bündeln und ein eigenes Quantencomputer-Team unter dem Radar der Öffentlichkeit zusammenstellen.
Im Juni 2020 nahm Honeywell den Quantencomputer H0 mit 6 Qubits in Betrieb und veröffentlichte eine wissenschaftliches Arbeit dazu xliii. Dank der Qubit-Güte und der vollen Konnektivität der Qubits war der H0 mit einem Schlag der Quantencomputer mit dem größten Quantenvolumen. Im Benchmark erzielte Honeywells System den Wert 64. Nur wenige Monate danach nahm Honeywell einen verbesserten Quantencomputer, mit 10 Qubits und einem Quantvolumen von 128, in Betrieb.
Honeywell verwendet für seine Ionenfallen-Quantencomputer eine 2 dimensionale Struktur, die es erleichtern soll in Zukunft mehrere Ionenfallen miteinander zu verbinden. Für diesen Zweck sind Honeywells Ionen auch nicht ortsgebunden, sondern werden über Radiowellen durch die Ionenfalle zu einem „Interaktionsbereich“ bewegt, in denen die 1-Qubit- und 2-Qubit-Quantengatter ausgeführt werden. Über diesen Weg kann insbesondere jedes Qubit mit jedem anderen Qubit verschaltet werden. Eine Besonderheit von Honeywells Quantencomputern ist, dass als „Ionen“ tatsächlich ein Verbund von 2 Ionenpaaren Yb-Ba verwendet werden. Die Ba-Ionen werden nur zur Kühlung bzw. zum Abbremsen der Yb-Ionen benötigt. Indem Honeywell aber jeweils 2 Yb-Ionen für ein Qubit verwendet, kann der Zustand des einen Yb-Ions ausgemessen werden und das Resultat der Messung kann wieder in das Quantenprogramm einfließen. Honeywell bezeichnet dies als „If-Statement“, das auch in der klassischen Programmierung verwendet wird. Dieses Feature war ein absolutes Novum unter den aktuell entwickelten Quantencomputern und ist eine wichtige Voraussetzung für zukünftige Algorithmen zur Quantenfehlerkorrektur.
Wie bei den anderen Anbieter, erreicht man Honeywells Quantencomputer per Fernzugriff. Ein entsprechender Zugang kann per Formular beantragt werden. Zur Programmierung wird aktuell die Sprache „OpenQASM“ verwendet, die ursprünglich von IBM vorgeschlagen hatte und einen Assembler-artigen Syntax besitzt. Ein eigenes Software-Team hat Honeywell nicht, sondern koorperiert zur Evualierung der Hardware mit verschiedenen Startups im Bereich Quantencomputing.
Aus dem Stand heraus ist Honeywell also ein Turbostart in die Riege der Quantencomputer-Hersteller gelungen: Vom „No-Name“ zu einem führenden Anbieter mit einem Quantenvolumen-Rekord von 128. Allerdings sah es zunächst so aus, als ob dieser Rekord nur wenige Tage halten würde …
IonQs Ionenfallen-Quantencomputer
Bereits seit den 1990ern ist Christopher Monroe von der University of Maryland ein führender Wissenschaftler für Ionenfallen-Quantencomputer. Dort entwickelte er zusammen mit seinem Team einen experimentellen 11 Qubit Ionenfallen-Quantencomputer in Laborgröße. Anders als andere Teams verwendete er für die Benchmark-Tests keine rein akademischen Quantenschaltungen, sondern Quantenalgorithmen aus dem Lehrbuch. Also kleine Quantenprogramme, die eine sinnvolle Berechnung ausführen. Zum Einen konnten sie den Bernstein-Vazirani-Algorithmus mit allen 11 Qubits ausführen: Dieser ermittelt mit einem einzigen Aufruf für eine Binärfunktion den „geheimen Schlüssel“, eine Bit-Sequenz aus 0en und 1en, welche die Binärfunktion erzeugt xliv. Das gleiche Problem spielt übrigens auch, auf abgewandelter Weise, die zentrale Rolle im Quantenvorteils-Arbeit für NISQ-Quantencomputer von IBM und der Universität München (s.o.). Außerdem konnte Monroes Team das sogenannte „Hidden-Shift“-Problem lösen, das auf klassischen Computern einen exponentiellen Aufwand besitzt xlv.

Frühes Bild von Christopher Monroe in einem Labor, Quelle Marym1234 / Wikipedia
Einen guten Einblick in die Arbeit bekommen Sie über Monroes packenden Vortrag aus dem Jahr 2018 xlvi. Darin geht er auch auf seine Firma IonQ ein:
Bereits vor einigen Jahren startete Monroe eine Kooperation mit Jungsang Kim von der Duke University, der besonders auf die Miniaturisierung von Ionenfallen-Quantencomputern spezialisiert ist. Zusammen entwickelten sie u.a. Strategien, wie man mehrere Ionenfallen über Photonenbrücken, also mittels Lichtteilchen, zu einem skalierbaren Ionenfallen-Quantencomputer koppeln könnte xlvii. Aus dieser Zusammenarbeit wurde IonQ im Jahr 2015 gegründet. Ziel war es dabei zunächst den experimentellen 11 Qubit-Quantencomputer aus Maryland in eine Miniaturform zu überführen und als kommerzielles Produkt anzubieten. Letzteres geschah im August 2020 über den zeitgleich gestarteten neuen Cloud-Dienst „Amazon Braket“. Einige Monate zuvor hatte die Firma Details zum Quantencomputer und zu den Benchmarks bereits in einer wissenschaftlichen Arbeit veröffentlicht xlviii.
Aktuell fokussiert sich IonQ darauf die Hardware-Entwicklung voranzutreiben. Der Zugriff auf IonQs Systeme erfolgt über die neuen Cloud-Dienste von Amazon und von Microsoft, über die Quantencomputer von verschiedenen Herstellern erreichbar sind. Beide Angebote stelle ich weitere unten genauer vor.
Wenige Tage nachdem Honeywell den Quantenvolumen-Rekord mit dem 10 Qubit-System H1 bekannt gab, kündigte IonQ im Oktober 2020 einen neuen Quantencomputer mit 32 Qubits an. Da der Hardwareansatz vergleichbar mit dem von Honeywell ist, kann man bei IonQs neuen Quantencomputer von einem Quantenvolumen von über 4 Mio ausgehen! Dabei erkennt man auch, dass die Maßeinheit „Quantenvolumen“ wohl bald zu unhandlich wird. IonQ setzt sich deshalb auch dafür ein, in Zukunft die Einheit „Algorithmische Qubits“ zu verwenden. Die Meldung hatte aber einen Schönheitsfehler: Abgesehen von der Ankündigung, gab es bis heute weder eine wissenschaftliche Veröffentlichung mit den Details über den neuen Quantencomputer, noch ist die neue Hardware verfügbar. Es mag zwar nur eine Frage der Zeit sein aber bis jetzt hat Honeywells Rekord weiterhin Bestand.
Wie auch IBM und Google stellte IonQ im Herbst 2020 eine Hardware Roadmap vor xlix. Laut der Roadmap rechnet IonQ die nächsten Jahre mit den algorithmischen Qubits. Danach plant die Firma, logische, fehlerkorrigierte Qubits zu verwenden. Aufgrund ihrer Qubit-Güte und deren vollen Konnektivität geht IonQ davon aus, dass einfachere Algorithmen für die Quantenfehlerkorrektur hierfür ausreichen werden. Laut Roadmap planen sie im Jahr 2025 64 fehlerkorrigierte Qubits und im Jahr 2026 bereits 256 fehlerkorrigierte Qubits bereitstellen zu können. Die dafür notwendige Fehlerkorrektur käme mit einem Verhältnis von 16:1 und danach mit 32:1 aus (Verhältnis physische Qubits zu logischen Qubits). Zum Vergleich: Google und IBM planen mit Quantenfehlerkorrekturen, die ein Verhältnis in der Größenordnung 1000:1 benötigen. Dies wäre also eine enorme Ersparnis und es bleibt abzuwarten, wie sich das in der Praxis verhält.
Nun wird es allerhöchste Zeit, dass wir uns dem absoluten Pionier für kommerzielle Quantencomputer widmen …
D-Waves Quanten-Annealer

Der allererste kommerzielle Quantenchip mit 128 Qubit-Chip, Quelle: D-Wave Systems, Inc., Wikipedia
Im Jahr 2011 hallte ein großer Paukenschlag durch die Technologiewelt: Die bis dahin allgemein unbekannte kanadische Firma „D-Wave-Systems“ präsentierte den ersten kommerziellen Quantencomputer auf Supraleiterbasis. D-Wave-Systems benannte die Anzahl der Qubits in seinem ersten Quantencomputer mit sage-und-schreibe 128 Qubits! Die Nachricht über D-Waves Quantencomputer sah also auf den ersten Blick so aus, als wäre damit der Durchbruch erzielt worden. Es kam noch besser: Im Jahr 2013 kauften Google und die NASA für mehrere Millionen Dollar ein Nachfolgemodell von D-Wave mit sagenhaften 512 Qubits!
Die Ära der Quantencomputer hatte also anscheinend mit Pauken und Trompeten begonnen.
Was in diesen Nachrichten ziemlich unterging, aber was allen Kennern der Thematik klar war: Der Quantencomputer von D-Wave-Systems war und ist streng genommen „nur“ ein Quanten-berechnendes System für spezielle Zwecke. Er nutzt zwar auch die Quantenmechanik mittels Qubits für Berechnungen aber er ist kein „universeller“ Quantencomputer, wie die Systeme, die ich Ihnen bis jetzt vorgestellt habe. Insbesondere können auf ihm nicht die typischen Lehrbuch-Algorithmen für Quantencomputer ausgeführt werden. Der Quantencomputer von D-Wave-Systems ist „nur“ für Optimierungsaufgaben vorgesehen (bzw. genauer für „quadratisch binäre“ Optimierungsprobleme l), also einem sehr wichtigen Aufgabengebiet für Computer, das sich insbesondere auf viele Bereiche übertragen lässt li. Der Computer von D-Wave ist ein sogenannter „Quanten Annealer“ (oft auch etwas ungenauer als „adiabatischer Quantencomputer“ bezeichnet). Er verlagert das Prinzip der sogenannten „simulierten Abkühlung“ (engl. simulated annealing) in die Quantenwelt. lii liii
Das Prinzip der „simulierten Abkühlung“ ist eine ziemlich brillante Rechentechnik für herkömmliche Computer, die insbesondere in der künstlichen Intelligenz eingesetzt wird. Interessanterweise stammt die Vorlage dazu wiederum aus der Physik bzw. der Metallurgie: Durch das Erhitzen eines Materials und anschließend kontrollierter Abkühlung werden die Eigenschaften des Ausgangsmaterials (z.B. die Festigkeit) optimiert: Das Material kann über spontane, thermische Sprünge aus einem Zustand mit schlechtem, lokalem Optimum in einen Zustand mit gutem, globalem Optimum gelangen liv.
Die Quantenversion dieses Prinzips simuliert im Gegensatz dazu keine langsame Abkühlung. Stattdessen startet ein adiabatischer Quantencomputer zunächst auf der „grünen Wiese“. D.h. die Qubits des Quantencomputers werden in einen Zustand versetzt der ein evtl. stark vereinfachtes Optimierungsproblem löst. Das tatsächliche Optimierungsproblem, also die eigentliche Berg-Tal-Charakteristik wird dann langsam und störungsfrei („adiabatisch“) dazugeschaltet. Ein adiabatischer Quantencomputer überbrückt die Optimierungstäler ebenfalls. Allerdings führt er keine thermischen Sprünge aus, sondern „tunnelt“ durch Quantenfluktuationen in das globale Optimum lv.
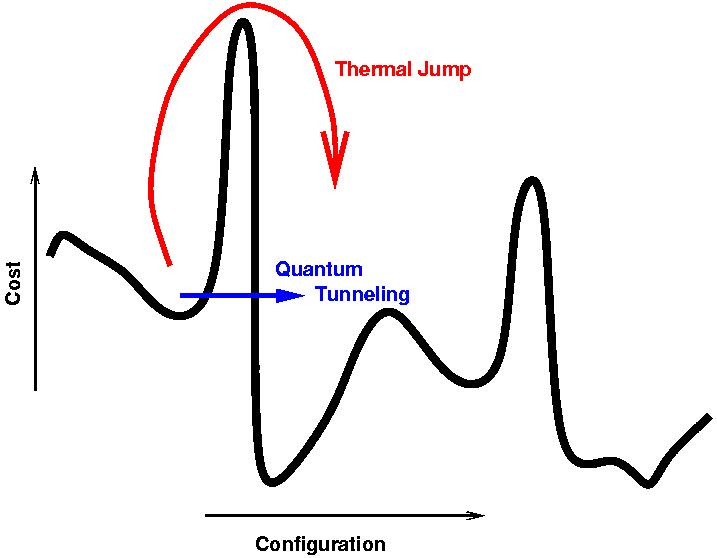
Die Täler sind die verschiedenen lokalen Optima, Quelle: Arnab Das / Wikipedia
Ein „Quanten Annealer“ wiederum ist ein adiabatischer Quantencomputer unter realen Bedingungen (z.B. unter Temperatureinflüssen und nicht perfekt isoliert). Insbesondere ist die Qubit-Güte wesentlich geringer, als die der Mitkonkurrenten. Aus D-Waves Sicht, reicht sie für das Annealing aber aus.
Wie ich oben schon erwähnt hatte: Ein universeller Quantencomputer verwendet Quantengatter, welche die Quantenlogik abbilden (z.B. H, X, Y, Z, CNOT). Im Gegensatz dazu verwendet D-Wave für seine „Quanten-Annealer“ , einen anderen Satz an Logikbausteinen, um die Qubits miteinander zu verschalten. Dieser Satz von analogen Quantenbausteinen, bildet gerade die adiabatische Quantenprogrammierung ab lvi. Interessanterweise wurde mittlerweile, in der Theorie nachgewiesen, dass auch mit den Logikbausteinen für adiabatische Quantenprogrammierung ein universeller Quantencomputer simuliert bzw. emuliert werden kann. Dies gilt allerdings nur unter perfekten Bedingungen. Die realen Quanten-Annealer sind hierzu nicht in der Lage.
Aus technischen Gründen kann D-Wave noch nicht alle Qubits miteinander verschalten. Stattdessen ordnete D-Wave die Qubits zunächst in einem sogenannten „Chimera-Graphen“ an, in denen jedes Qubit mit insgesamt 6 Nachbar-Qubits verschaltet werden kann lvii. Im Jahr 2019 führte D-Wave eine verbesserte Graphen-Topologie ein: Die „Pegasus-Graphen“ lviii. Durch die neue Struktur wird jedes Qubits mit bis zu 15 anderen Qubits verschaltet. Diese Kopplungsstärke ist sehr entscheidend: Jede Einschränkung reduziert die Anzahl der tatsächlich verfügbaren Qubits in der Praxis teils deutlich (so sind in der Chimera-Topologie z.B. einige zyklische Kopplungen nicht direkt möglich). Um solche Kopplungen doch zu erreichen fasst D-Wave mehrere Qubits zu einem logischen Qubit teils automatisch zusammen („embedding“).
Im Laufe der Jahre hat D-Wave seine Palette an Quanten-Annealer erweitert. Seit September 2020 bietet die Firma das Modell DWave-Advantage mit 5000 Qubits an. Zwar hat D-Wave mittlerweile ein paar Quantencomputer für einige Millionen Dollar an einzelne Kunden verkauft (z.B. Google, die NASA, demnächst auch das Forschungszentrum Jülich), interessanter ist für einen größeren Kundenkreis allerdings D-Waves Cloud-Angebot „Leap“ lix. Hier ist u.a. eine Trialmitgliedschaft möglich, mit einem kostenlose Guthaben von Netto-Runtime-Zeit auf den Quantenchips (QPU).
Um eigene Quantenprogramme zu erstellen bietet D-Wave eine eigene Software-Palette an. Kernstück bildet hier das Python-Framework „Ocean“ lx. Das Framework abstrahiert die eigentlich RESTful-Schnittstelle zum Quanten-Annealer und ermöglich zusätzlich die lokale Simulation von Quantenprogrammen auf dem eigenen Rechner.
Aufbauend darauf stellt D-Wave u.a. das Programm „qbsolv“ bereit. „qbsolv“ zerlegt ein allgemeines „QUBO“-Optimierungsproblem (steht für „Quadratic Binary Optimization“) automatisch in kleinere Häppchen und bildet diese auf die Chimera- oder die Pegasus-Struktur des jeweils verwendeten Quantenrechners ab. In mehreren Durchläufen versucht „qbsolv“ das Ergebnis immer weiter zu verbessern lxi. Über den neuen „Hybrid-Solver“ können außerdem Aufgaben an Leap gesendet werden, die wesentlich mehr als die 5000 binären Freiheitsgrade des QPUs besitzen. Durch das Zusammenspiel mit herkömmlichen Rechenroutinen kann Leap dadurch laut D-Wave bis zu 1 Millionen Variablen verarbeiten.
Die Erfolgsstory von D-Wave und ein Schönheitsfehler daran
Im Laufe der Zeit hat D-Wave weitere Kontrollmöglichkeiten für die Quanten-Annealer hinzugefügt: Das „Scheduling“ bietet die Möglichkeit, den Zeitplan zu beeinflussen, mit dem das eigentliche Optimierungsproblem dazugeschaltet wird. Gerade an den kritischen Stellen, kann eine Verlangsamung entscheidend werden. Über das „Reverse Annealing“ wiederum kann man verbesserte Start- oder Zwischenzustände erzeugen: Dazu spult D-Wave das Annealing für kurze Zeit rückwärts ab, um es dann wieder vorwärts laufen zu lassen.
D-Wave verantstaltet teils halbjährig eigene Usergroup-Konferenzen „D-Wave Qubits“ lxii mit Erfahrungsberichten von D-Wave-Kunden (darunter VW, Airbus u.a. Großkonzerne). Die Latte der Usecases (D-Wave benennt aktuell die Zahl: 250) ist beeindruckend und andere Hardware-Hersteller kommen da aktuell nicht einmal ansatzweise heran. Tatsächlich sind derzeit nur D-Waves Quanten-Annealer dank ihrer 5000 Qubits in der Lage, „real-life“ Usecases zumindest in Teilen umzusetzen (in VWs Fall z.B. ein Verkehrsleitungssystem lxiii).
Die Sache hat allerdings einen Haken: Anders als für universelle Quantencomputer konnte man für Quanten-Annealer in der Theorie bis dato noch keinen generellen „Quantenvorteil“ gegenüber klassischen Computern voraussagen. D.h. über universelle Quantencomputer weiß man, dass sie gegenüber herkömmlichen Supercomputern einen teils gewaltigen Rechenvorteil besitzen, sobald sie nur groß genug skaliert werden. Damit meine ich gerade die typische Eigenschaft der Quantencomputer: Mit jedem weiteren Qubit verdoppelt sich das Leistungspotential. Von Quanten-Annealern ist dies nur für einen kleinen Problembereich bekannt lxiv. Überdies haben Forscher mit den Algorithmen für Quantenfehlerkorrektur einen Mechanismus entdeckt, mit dem man universelle Quantencomputer hochskalieren kann. Etwas Vergleichbares ist für Quanten-Annealer noch nicht bekannt. Trotz dieser Bedenken gibt es einige erfolgversprechende Arbeiten aus der Praxis lxv.
Xanadus photonischer CV-Quantencomputer
Einen sehr spannenden und ganz anderen Ansatz als die bisher vorgestellten, verfolgt das kanadische Startup Xanadu lxvi.
Neben supraleitenden Qubits und Ionenfallen-Quantencomputer gibt es einen weiteren sehr naheliegenden Architekturansatz: Ein Quantencomputer mittels Photonen, also Lichtteilchen. Lichtteilchen sind elektrisch neutral, reagieren deshalb nur wenig mit ihrer Umgebung und können einen Quantenzustand lange aufrecht halten (im Weltall sogar über Lichtjahre). Insbesondere können photonische Qubits auch bei Raumtemperatur betrieben werden. Hinzu kommt, dass sich seit ein paar Jahren eine neue aber schnell wachsende Technologie entwickelt hat, die sich „Integrated Photonics“ nennt lxvii. Wie für supraleitende Qubits können hierüber integrierte Schaltkreise über bestehende industrielle Fertigungstechniken konstruiert werden. Bei Integrated Photonics werden allerdings keine elektrischen, sondern optische Schaltkreise verwendet.
Um einen universellen, photonischen Quantencomputer zu entwickeln, gibt es zwei Alternativen: Lineare optische Quantencomputer, die das sogenannte „KLM-Protokoll“ verwenden und Continuous-Variable-Quantencomputer („CV“). Bei ersteren funktioniert das Quantencomputing analog zu den bisher vorgestellten Quantencomputern mit einer festen Anzahl filigraner photonischer Qubits, die miteinander über Quantengatter in Form von Interferometer verschaltet werden. Diesen Ansatz verfolgt zum Beispiel die Firma „PsiQuantum“ um den Quanten-Photonics-Pionier Jeremy O’Brien von der Universität Bristol. Abgesehen von ein paar spannenden Vorträgen auf Youtube und Meldungen zu Fundraising-Rekorden dringt allerdings aus der Firma nichts nach außen (noch nicht einmal eine Website) lxviii lxix.
Der andere photonische Ansatz wird von der Firma Xanadu aus Kanada verfolgt, die im September 2020 ihr Cloud-Angebot vorstellte. Xanadus Quantencomputer arbeiten nicht mit einzelnen Photonen, sondern mit Photonenstrahlen: Hierzu werden Laserstrahlen durch Resonatoren geleitet, die aus dem Licht einen sogenannten „Squeezed“ Quantenzustand bilden lxx lxxi: Eine quantenmechanische Überlagerung aus vielen Photonenpaaren. Diese gebündelten Zustände sind die zentralen Informationseinheiten in Xanadus Quantencomputern. Anstelle von Qubits mit zwei diskreten Zuständen besitzen solche „Qumodes“ ein kontinuierlichen Spektrum von beliebig vielen Zuständen. Deshalb spricht man hier von „Continuous-Variable“-Quantencomputern. Xanadus erste Quantencomputer-Familie X8, die Firma hat mehrere Geräte dieses Typs, arbeiten mit 8 solcher Qumodes. Kurz nach dem Start kündigte Xanadu an, diese Größe jedes halbe Jahr zu verdoppeln. Mittlerweile gibt es Quantencomputer vom Typ X12, X24 und ein X40-Modell wurde bereits angekündigt. Die darauf folgende Hardware-Reihe soll Qumodes mit vollständiger Konnektivität ermöglichen lxxii.
Ein CV-Quantencomputer ist auch universell, arbeitet aber mit einem anderem Satz an Standard-Quantengattern, die die Zustandsübergänge in dem kontinuierlichen Spektrum steuern. Xanadu verwendet hierfür programmierbare Mach-Zehnder-Interferometer lxxiii über die z.B. Beam-Splitting und Phasenverschiebungen des Strahls gesteuert werden. Ein spannender Anwendungsfalls für Xanadus Quantencomputer ist das sogenannte „Boson Sampling“. Das Boson Sampling ist eines der Kandidaten um mit aktuellen Mitteln eine Quantenüberlegenheit zu erzielen (s. den Abschnitt zu Google) lxxiv. Im Fall von Xanadus Quantencomputer bedeutet dies konkret: Die Häufigkeiten von Photonen zu messen (Photonen zählen auch zu den „Bosonen“). Hierzu stellte Xanadus Software-Team ein paar interessante Anwendungsfälle vor, unter anderem das „Dense-Subgraph“-Problem lxxv lxxvi. Das Boson Sampling stelle ich nochmal im folgenden Abschnitt zu Chinas Quantencomputer näher vor, da es dort eine enscheidende Rolle spielt.
Überhaupt ist Xanadus Software-Team ziemlich fleißig. Mit „Strawberry Fields“ hat es einen sehr gut dokumentierten Framework entwickelt über den die CV-Quantencomputer ferngesteuert werden (ebenfalls auf Basis der beliebten Programmiersprache Python) lxxvii.
Wie für die anderen Herstellern ist die NISQ-Ära für Xanadu nur eine Übergangsphase und das eigentliche Ziel ist es, fehlerkorrigierte Quantencomputer zu konstruieren. Für CV-Quantencomputer wurde bereits vor vielen Jahren sogenannte GKP-Zustände vorgeschlagen lxxviii (benannt nach den Entdeckern, die „Godfathern“ der Quantenfehlerkorrektur Gottesmann, Kitaev und Preskill). Ziel ist es dabei Lichtbündel mit einem schachbrettartigen Spektrum zu erzeugen. Je nach Lage des Spektrums stellt es ein „Qubit“ im Zustand „0“ oder etwas verschoben ein Qubit im Zustand „1“ dar lxxix. Leichte Verformungen bzw. Verschiebungen des Gitters könnte man relativ verlässlich korrigieren. Wie Xanadu das alles realisieren will, stellte das Team 2020 in einer wissenschaftlichen Arbeit vor lxxx lxxxi. Die Hardware kann nur zufällig entweder die aktuell verwendeten „Squeezed“-Lichtbündel oder die gewünschten GKP-Zustände erzeugen. Erstere sollen dann aus dem Chip geleitet werden, so dass am Ende nur noch die GKP-Zustände übrig bleiben. Laut Xanadu ist die Photonik für die endgültige Skalierung der Quanten-Chips der aussichtsreichste Kandidat. Anders als für supraleitende Qubits und Ionenfallen konnten hier bereits Verschränkungen von Zehntausenden bis zu Millionen Photonen experimentell bestätigt werden. Für die Kopplung von mehreren Quanten-Chips sollen Photonen auch bei anderen Architekturen die die Quantenzustände vermitteln. In Xanadus Quantencomputer wäre das ganz ohne „Medienbruch“ möglich.
Chinas Photonischer Quantencomputer und die Quantenüberlegenheit
Im Frühjahr 2018 berichtete ich an dieser Stelle über ein überraschendes Cloud-Angebot des chinesischen Tech-Riesens Alibaba: Ein supraleitender 11-Qubit Quantencomputer lxxxii lxxxiii. Zwar forscht ein Team bei Alibaba weiterhin im Bereich Quatencomputing lxxxiv aber das Cloud-Angebot ist verschwunden. Die Seite zeigt nur noch Schriftzeichen an und dafür ist mein Chinesisch wohl zu eingerostet :-).
Mittlerweile machte aber ein ganz anderes chinesisches Quantencomputer-Projekt weltweite Schlagzeilen: Im Dezember 2020 meldete ein chinesisches Team um den Quanten-Forscher Jian-Wei Pan, von der University of Science and Technology of China, in der renommierten Fachzeitschrift Science einen Durchbruch lxxxv. Ähnlich wie Googles Team ein Jahr zuvor gelang es der Gruppe auf ihrem photonischen Apparat eine Rechenaufgabe in 200 Sekunden zu bewältigen, für die ein Supercomputer sage und schreibe 2,5 Milliarden Jahre benötigt hätte!

Eingangstor zur University of Science and Technology of China, Quelle Ryanli / Wikipedia
Anders als Googles „Sycamore“-Quantencomputer ist der chinesische Quanten-Apparat in Laborgröße weder ein universeller Quantencomputer noch ist er programmierbar, sondern besitzt einen festen Aufbau von Beam-Splittern, Spiegeln und Prismen, durch den Laserstrahlen geschickt werden. Pans Versuchsaufbau ist letztendlich eine „Boson Sampling“-Aufgabe.
Das Boson Sampling ist eines der Kandidaten, um mit aktuellen Mitteln eine Quantenüberlegenheit gegenüber herkömmlichen Computern zu erzielen. Der Forscher Scott Aaronson, den ich hier schon mehrfach erwähnt habe, hatte das Prinzip bereits 2011 mit seinem Kollegen Alex Arkhipov vorgeschlagen: Schickt man einen Strahl mit einer bestimmten Anzahl Lichtteilchen / Photonen (die nebenbei zu den Bosonen gehören), durch einen Quanten-Interferometer, der jedes einzelne Photon in viele unterschiedliche Quanten-Zustände aufteilen kann, ergibt sich für den kompletten Strahl schnell eine astronomisch hohe Zahl an Zustandskonfigurationen lxxxvi. Den chinesischen Forschern gelang es konkret einen Strahl mit 50 Photonen kontrolliert durch einen 100-Moden-Interferometer zu senden und die Photonenzahl für jede Mode über Photodetektoren zu zählen. Der Clou dabei ist: Aaronson und sein Kollege konnten seinerzeit beweisen, dass man die gemessene Häufigkeitsverteilung für solche quantenmechanische Boson-Sampling-Apparate auf herkömmlichen Computern nur einem astronomischen Aufwand berechnen kann lxxxvii. Im Gegensatz dazu kann der Apparat selbst einfach angepasst und prinzipiell auch „programmiert“ werden. Und genau darum geht es letztendlich bei Quanten-Überlegenheit.
Jian-Wei Pan ist vermutlich der international renommierteste chinesische Forscher für Quanteninformation lxxxviii. Seinen Doktortitel bekam er in Österreich bei Anton Zeilinger, der schon für seine Pionierarbeiten zur Quanten-Teleportation für den Nobelpreis vorgeschlagen wurde, und der früher nebenbei ein Kollegen der beiden Innsbrucker Forscher Zoller und Cirac war. Für Aufsehen sorgte Pan bereits 2017, als es seinem Team gelang eine Quantenverschränkung per Satelliten herzustellen und damit eine quantenverschlüsselte Kommunikation zwischen Peking und Wien einzurichten.
Wie nach Googles Nachweis der Quanten-Überlegenheit erzeugte die Veröffentlichung des chinesischen Teams eine rege Betriebsamkeit unter Forschern. Unter anderem stellte diesmal Googles Team das Ergebnis zumindest in Teilen in Frage. Unbestritten ist, dass das Experiment der bis dato bei weitem größte Boson-Sampling-Apparat ist, der jemals gebaut wurde. Unbestritten ist auch, dass man prinzipiell damit in der Lage wäre einen weiteren Nachweis der Quantenüberlegenheit durchzuführen. Mittlerweile ist sich aber sogar Scott Aaronson nicht mehr sicher, der nebenbei der Gutachter für den Science-Artikel war, ob das „Rauschen“ der Fehlerquellen bei dem Experiment am Ende doch noch eine klassische Simulation möglich machen würde lxxxix.
Die Quantencomputer-Cloudangebote von Microsofts und Amazon

Microsoft Campus in Redmon, Quelle: Coolcaesar / Wikipedia
Im Jahr 2018 berichtete ich an dieser Stelle von Microsofts ambitionierten Quantencomputer-Ambitionen. In dem Vorhaben einen „topologischen“ Quantencomputer mit eingebauter Quantenfehlerkorrektur zu konstruieren, wagten sie sich weiter in Grenzbereiche der Grundlagenforschung vor, als alle anderen Hersteller xc. Mittlerweile hat das Projekt allerdings einen herben Rückschlag erlitten und es ist abzuwarten, wie Microsoft hierauf reagiert xci.
Parallel zur dieser Entwicklung hat sich Microsoft allerdings längst als Cloudanbieter und „Reseller“ für Quantencomputer positioniert: Mit „Azure Quantum“ bietet der Konzern seit Februar 2021 einen Preview-Zugang auf die Quantencomputer von Honeywell und IonQ an.
https://azure.microsoft.com/de-de/services/quantum/
Microsoft bezeichnet Azure Quantum als „Offenes Ökosystem“ über das Anwender auf die Hardware- und Softwarelösungen von Microsoft und Partnern zugreifen können. Neben den oben genannten Quantencomputern ist dies aktuell ein GPU-gestützter Service von Toshiba, um mithilfe von herkömmlichen Computern Optimierungsprobleme zu lösen. Außerdem nennt Microsoft hier Softwarelösungen des kanadischen Startups 1Qubit und die „quanten-inspirierten“ Lösungen von Microsoft selbst. Darunter versteht man Algorithmen für herkömmliche Computer, die Quanteneigenschaften teilweise „simulieren“, wie z.B. das Tunneln der „Kostenberge“ beim Simulated Annealing (s.o.). Unter anderem hierfür hatte der Tech-Riese bereits vor Jahren renommierte Forscher für sich gewinnen können. Die Softwarelösungen sind fertige Pakete für die man insbesondere kein Knowhow in Quantencomputing benötigt xcii.
Bereits im Herbst 2017 veröffentlichte Microsoft die Erweiterung „Q#“ („Qu-Sharp“) xciii für seine bekannte Programmierumsprache „C#“ mit denen Quantenprogramme erstellt und auf herkömmlichen Computern simuliert werden können. Anders als die Python-Frameworks der anderen Quantencomputer-Anbieter besitzt Q# einen ganz eigenen Syntax. Dieser soll es in Zukunft erleichtern, die sehr spezifischen Hardwaredetails in Quanten-Programmen zu abstrahieren. Mittlerweile kann Q# in diversen Entwicklungsumgebungen, wie Microsofts „Visual Studio“ als auch per Zusatz-Plugin für das, im wissenschaftlichen Umfeld, beliebte Jupyter-Notebook verwendet werden. Neben der Software stellt Microsoft eine reichhaltige Dokumentation für den Einstieg in das Quantencomputing und für diverse Quanten-Algorithmen bereit.
09

Logo von Amazon Web Services, Quelle: Amazon.com Inc. / Wikipedia
Im August 2020 betrat ein weiterer Tech-Riese den Ring: Mit „Amazon Braket“ startete Amazon einen eigenen Cloud-Dienst für Quantencomputer.
https://aws.amazon.com/de/braket/
Amazon ist im Bereich Quantencomputing bis dahin noch nicht in Erscheinung getreten. Entsprechend baut der Konzern zunächst auf die Dienste und das Knowhow von Partnern. Über Amazon Braket, das „Braket“ im Namen verweist übrigens auf die Dirac‘sche Klammerschreibweise von Quantenzuständen, können die Quantencomputer von D-Wave, IonQ und Rigetti erreicht werden. Hinzu kommen Simulatoren für Quantenprogramme. Amazon Braket ist Bestandteil von Amazon‘s Cloudangebot AWS und intergriert sich nahtlos in das breite Spektrum der übrigen AWS-Dienste (dies gilt übrigens auch für Microsofts Azure Quantum). Zum Fernsteuern des Angebots bietet der Konzern ein „Amazon Braket Software Development Kit“ für die Programmiersprache Python an. Im Falle von D-Waves Quanten-Annealers basiert das Braket SDK dabei auf dem Ocean SDK von D-Wave, das ich bereits weiter oben erwähnt habe.
Mit dem „Amazon Quantum Solutions Lab“ hat der Tech-Riese außerdem eine enge Zusammenarbeit mit dem California Institute of Technology (Caltech) gestartet, einer der führenden Hochschulen im Bereich Quantencomputing, und koorperiert von dort unter anderem mit verschiedenen Startups im Bereich Quantencomputing-Software. Das Solutions Lab soll Kunden und Anwender beim Einstieg in das Quantencomputing und bei Projektarbeiten unterstützen. Mittlerweile mehren sich außerdem die Hinweise, dass Amazon damit begonnen hat, an einer eigenen Quantencomputer-Hardware zu arbeiten.
Fußnoten
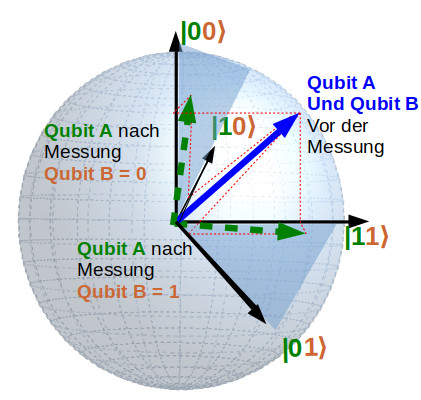
i Die Lehrbuch-Darstellung eines Qubits verwendet die sogenannte „Blochsphäre“. Diese gibt alle Freiheitsgrade eines 1-Qubit-Systems exakt wieder.
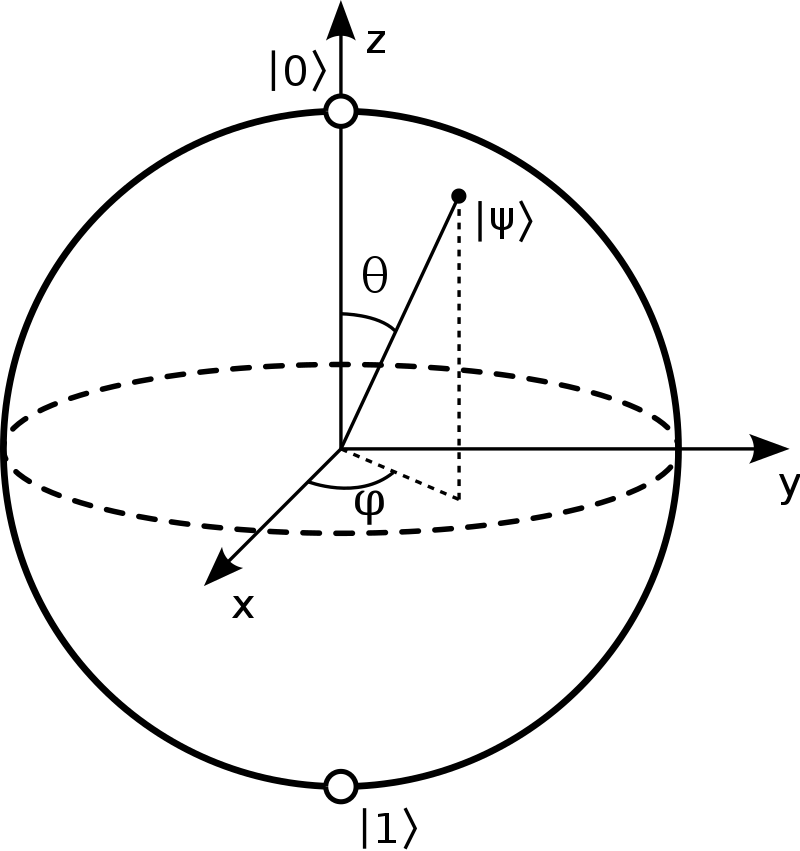
Quelle: Glosser.ca / Wikipedia
Allerdings lässt sie sich nicht einfach auf Mehr-Qubit-Systeme verallgemeinern. Insbesondere verhält sich ein Zwei-Qubit-System gerade nicht wie zwei Bloch-Sphären. In meiner vereinfachten Darstellung lässt sich eher erahnen, wie es mit steigender Qubitanzahl weitergeht:
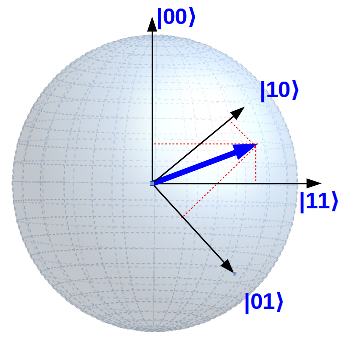
Vereinfachte Darstellung eines Zwei-Qubit-Systems
ii https://quantumcomputing.stackexchange.com/questions/3860/how-many-qubits-are-simulable-with-a-normal-computer-and-freely-accessible-simul: Forum-Beitrag „How many qubits are simulable with a normal computer and freely accessible simulators?“ auf Quantum Computing Stack Exchange bei dem man einen ersten Eindruck bekommt.
iii Um einen Quantencomputer mit etwa 250 Qubits zu simulieren, müsste man jedes Atom des Weltalls in ein Bit für herkömmliche Computer umwandeln.
iv Die T1-Decoherence-Time misst die durchschnittliche Zeit, für die Bit-Flip-Fehler auftreten können. D.h. das Qubit, das eigentlich im Zustand „1“ ist, wechselt in den Zustand „0“. Supraleiter-Qubits erzielen hier Werte im 100er Mikrosekunden-Bereich während Ionen-Qubits mehrere Stunden schaffen können. Die T2-Decoherence-Time ist die durchschnittliche Dauer, bis ein überlagertes Qubit seine relative Phase verliert (also „1“ + „0“ zu „1“ – „0“ wird). Bei supraleitenden Qubits sind T1- und T2-Zeiten vergleichbar. Ionen-Qubits schaffen hier Werte von 1 Sekunde. Die T1-Fehlerquelle gibt es im Prinzip auch bei herkömmlichen Computern, die T2-Fehlerquelle jedoch nicht.
v https://arxiv.org/abs/2006.02856: „The Bitter Truth About Quantum Algorithms in the NISQ Era“ wissenschaftliche Arbeit von Frank Leymann von der Universität Stuttgart über die Einschränkungen von aktuellen Quantencomputern und was das für Auswirkungen auf Lehrbuch-Quantenalgorithmen hat. Einen Vortrag von Frank Laymann zu der Arbeit finden Sie hier https://www.youtube.com/watch?v=z6zllSVvyu0
vi Einen Eindruck von der Fülle an wissenschaftlichen Arbeiten zu NISQ-Quantencomputer und ihren Anwendungen bekommen Sie im „NISQ Computing Newsletter“ vom „Research Institute for Advanced Computer Science“ https://riacs.usra.edu/quantum/nisqc-nl. Offen ist allerdings tatsächlich, ob sich aus diesen Arbeiten ein praktischer Quantenvorteile erzeugen lässt: Während die Roadmaps anderer Hersteller einen Quantenvorteil in der NISQ-Ära fast schon fest einplanen, hat Googles Quantencomputing-Forscher Guillaume Verdon im September 2020 eine informelle und vermutlich nicht repräsentative Umfrage gestartet „Odds that any party manages to discover and implement a truly quantum-advantageous industry-relevant application in the NISQ era“. Eine Mehrheit tendierte dabei zu „eher nicht“ https://twitter.com/quantumVerd/status/1306434913198112769. Als Rückschlag, gerade auch für die supraleitenden NISQ-Quantencomputer mit begrenzter Konnektivität, muss auch diese theoretische Untersuchung von IBM gewertet werden, die das Potential von herkömmlichen und Quanten-Computern vergleicht: https://www.ibm.com/blogs/research/2021/01/quantum-mean-values/.
vii https://www.youtube.com/watch?v=kE6lgJFYYLc: In dem Vortrag „Surveying the Quantum Computing Market Landscape“ auf der virtuellen Konferenz Quantum For Business 2020 stellte Bob Sorensen von der Hyperion Research, LLC eine detaillierte Analyse des Quantencomputer-Marktes vor. Darin erläuterte er unter anderem eine Umfrage über die kommenden Budget-Pläne von 130 nordamerikanischen Unternehmen. Der Umfrage zur Folge gaben 32% der Firmen an für 2019 überhaupt keine Ausgaben für das Quantencomputing eingeplant zu haben. Diese Zahl fällt bis 2024 auf unter 3% wohin gegen das Gesamtbudget für den Quantencomputing-Markt von 300 Mio. Dollar auf über 1 Milliarde Dollar steigt. Sicher bilden die befragten Firmen keinen repräsentativen Querschnitt durch die Volkswirtschaft aber ich denke, dass man die Tendenz verallgemeinern kann.
viii Eine schöne, detaillierte Beschreibung des „Quantum Volume“-Protokolls finden Sie auf den Pennylane-Seiten des Herstellers Xanadu https://pennylane.ai/qml/demos/quantum_volume.html (bzw. archiviert https://web.archive.org/web/20201216123226/https://pennylane.ai/qml/demos/quantum_volume.html)
ix https://www.scottaaronson.com/blog/?p=4649: Scott Aaronsons Blog-Post „Turn down the quantum volume“
xi Einen guten Einstieg in das Thema Supraleitende Qubits und Circuit QED bekommen Sie bereits auf Wikipedia: https://en.wikipedia.org/wiki/Superconducting_quantum_computing, https://en.wikipedia.org/wiki/Circuit_quantum_electrodynamics, https://en.wikipedia.org/wiki/Coplanar_waveguide
xii Da die Supraleiter-Technologie viele Architektur-Ansätze möglich macht, gibt es auch viele Artikel und Arbeiten dazu. Eine aktuelle Übersicht von 2020 finden Sie z.B. in https://arxiv.org/abs/2006.10433: Wissenschaftliche Arbeit „Superconducting Quantum Computing: A Review“ u.a. von der University of Science and Technology of China.
xiii In einem normalen Quantenschwingkreis sind die Zustände wie die Sprossen auf einer Leiter verteilt. Normalerweise würden die Zustände dadurch beliebig hoch- und herunterklettern. Durch die Josephson Junctions wird diese Leiter verformt. Die Zustände sind dadurch ähnlich wie in einem Atom verteilt. In Circuit QED spricht man daher von einem „künstlichen Atom“. Das „einfarbige“ Mikrowellenlicht, das die Übergänge zwischen dem Zustand „0“ und „1“ erzeugt, ist dadurch unsichtbar für alle weiteren Übergänge.
xiv https://www.youtube.com/watch?v=AqoKpUDchYo&list=PL5jmbd6SJYnPiYlM6pHAm2M3FL40D9otZ: Eine schöne Vortragsreihe „The Building Blocks of a Quantum Computer“ von kurzen Videos der TU Delft. Das Institut QuTech ist eine der ersten Adressen für das Quantencomputing innerhalb Europas.
xv https://www.youtube.com/watch?v=FklMpRiTeTA: Gefeierter Vortrag von John Martinis am Caltech „Quantum supremacy using a programmable superconducting processor“. Absolut sehenswert!
xvi https://en.wikipedia.org/wiki/Toric_code: Beschreibung des „Surface Code“ bzw. „Toric Code“ zur Quantenfehlerkorrektur auf Wikipedia. Der Surface Code ist ein sogenannter „topologischer“ Fehlercode, der physikalische Qubits zu geometrischen Gruppen mit bestimmten globale Eigenschaften zusammenfasst (z.B. eine einfache Schleife, eine zweifache Schleife, …). Diese geometrischen Eigenschaften sind quasi immun gegen kleinere, lokale Veränderungen.
xvii Das Ende der so erfolgreichen Zusammenarbeit von John Martinis und Google überraschte die gesamte Quanten-Gemeinde. Später erläuterte John Martinis die Hintergründe die dazu führten erstaunlich offen in einem Interview mit Forbes https://www.forbes.com/sites/moorinsights/2020/04/30/googles-top-quantum-scientist-explains-in-detail-why-he-resigned/ . Aktuell arbeitet Martinis mit dem australischen Startup Silicon Quantum Computing für Quantum-Dot-Qubits zusammen.
xviii https://www.youtube.com/watch?v=TJ6vBNEQReU&feature=youtu.be&list=PLQY2H8rRoyvx4VttfJOPRslw8XWT7yaBJ&t=967: Vortrag von Googles AI Quantum Team-Leader Hartmut Neven über die Roadmap seines Hardware-Teams (im Rahmen von Googles Quantum Summer Symposium Konferenz 2020)
xix https://www.youtube.com/watch?v=tY2L41VHI3I: Vortrag „Building a Practical Error-Corrected Quantum Computer in 10 Years“ von Googles Teamleitern auf der virtuellen Konferenz Quantum For Business 2020. Darin wird das Kern-Team nach John Martinis Abgang von Google vorgestellt. Außerdem erläutern Googles Forscher ihr erstes Nahziel: Zu prüfen, ob das Paradigma der Quantenfehlerkorrektur in der Praxis umgesetzt werden kann. Können physikalische Qubits zu einem logischen Qubit zusammengefasst werden und verbessert sich mit jedem weiteren physikalischen Qubit die Güte dieses logischen Qubits exponentiell?
xx https://quantumai.google/: Homepage von Google Quantum AI
xxi https://www.youtube.com/watch?v=fqI_IsQX6Kg: Vortrag „Quantum Applications Development at Google“ von Ryan Babbush im Dezember 2019
xxiii https://ai.googleblog.com/2017/10/announcing-openfermion-open-source.html: Googles Blog-Ankündigung zum Framework „OpenFermion“ https://github.com/quantumlib/OpenFermion
xxiv https://www.tensorflow.org/quantum: Homepage von TensorFlow Quantum. TensorFlow Quantum ist eine Cirq-Erweiterung von Googles beliebten AI-Framework TensorFlow,
xxv https://www.sciencedaily.com/releases/2001/12/011220081620.htm: Über IBMs experimentellen Beweis zu Shor‘s berühmten Algorithmus. In diesem Fall konnte IBM einen Mini-Quantencomputer konstruieren, der in der Lage war die Zahl 15 in die Faktoren 5 und 3 aufzuteilen. Dies mag zwar fast lächerlich erscheinen aber auf der anderen Seite war diese Arbeit der erste Hinweise darauf, dass der Algorithmus tatsächlich programmiert werden kann. Damals setzte man übrigens noch auf die NMR- bzw. Kernspin-Technologie, die man unter anderem aus Krankenhäusern her kennt. Später stellte sich dieser Ansatz allerdings als Sackgasse heraus.
xxvi https://www.youtube.com/watch?v=uk6d175AC7A: Vortrag „A View of the Road Ahead from IBM“ von IBMs Anthony Annunziata auf der virtuellen Konferenz Quantum For Business 2020. https://www.ibm.com/blogs/research/2020/05/quantum-challenge-results/, https://www.ibm.com/blogs/research/2020/04/ibm-quantum-challenge/ : Blog-Einträge von IBMs Quantum-Team die den Umfang und die Akzeptanz von IBMs Cloudangebot Quantum Experience verdeutlichen.
xxviii https://quantum-computing.ibm.com/composer/docs/guide/ : Userguide auf IBMs Quantum Experience
xxix https://qiskit.org/textbook/preface.html: Homepage zu IBMs Qiskit-Lehrbuch, ein sehr einfacher aber gelungener Einstieg in das Quantencomputing.
xxx https://www.ibm.com/blogs/research/2020/09/ibm-quantum-roadmap/: Blogeintrag von IBMs Quantum-Team zur Hardware-Roadmap für die nächsten Jahre.
xxxi https://www.ibm.com/blogs/research/2020/09/hardware-aware-quantum/: Blogeintrag von IBMs Quantum-Team über die zukünftige Qubit-Topologie und dem speziell dafür optimierten Algorithmus zur Quantenfehlerkorrektur.
xxxii https://www.ibm.com/quantum-computing/network/members: Mitglieder des IBM Quantum Network
xxxiii https://arxiv.org/abs/1904.01502: Wissenschaftliche Veröffentlichung „Quantum advantage with noisy shallow circuits in 3D“ u.a. von IBMs Sergey Bravyi, David Gosset und Robert König von der Technischen Universität München. Diese Arbeit belegt zumindest theoretisch, dass selbst mit NISQ-Quantencomputern ein Quantenvorteil gegenüber herkömmlichen Computern möglich sein müsste. Und anders als Googles „Random Circuit Sampling“-Algorithmus ist die betreffende Aufgabe ein „sinnvolles“ Problem: Finde den „geheimen“ Schlüssel, der eine spezielle mathematische Aufgabe löst. Die Komplexität des Problems wächst auf einem herkömmlichen Computer, selbst wenn diesem zusätzliche Prozessorkerne hinzugefügt werden. Auf einem NISQ-Quantencomputer bleibt die Komplexität dagegen konstant. Allerdings lässt sich dadurch noch keine praktische Anwendung ableiten und das Leistungspotential ist nur logarithmisch besser (ganz im Gegensatz zu Googles exponentieller Steigerung).
xxxiv https://www.rigetti.com: Homepage der Firma Rigetti Computing.
xxxv https://arxiv.org/abs/1801.03897: „Cloud Quantum Computing of an Atomic Nucleus“ Fachartikel
xxxvi https://en.wikipedia.org/wiki/Cirac%E2%80%93Zoller_controlled-NOT_gate: Wikipedias Artikel zu Cirac und Zollers Ansatz für ein CNOT-Quantengatter, eine zentrale und besonders herausfordernde Komponente jedes Quantencomputers. Die Ionenfallen-Quantencomputer, die ich in diesem Artikel erwähne, verwenden alle eine Weiterentwicklung dieses Ansatzes von Mølmer und Sørensen.
xxxvii https://www.quantiki.org/wiki/ion-traps: Sehr schöner und einfacher Überblick über Ionenfallen-Quantencomputer.
xxxviii http://research.physics.berkeley.edu/haeffner/publications/review-QC-IISc-090306.pdf: Detailliertere Artikel „Quantum computing with trapped ions“ von Hartmut Häffner (der ebenfalls aus dem Innsbrucker Team stammt). Beschreibt unter anderem die verschiedenen Ansätze für CNOT-Gatter und u.a. auch den Mølmer-Sørensen-Ansatz.
xxxix Zwar ist es nicht möglich ein einzelnes geladenes Atom in einem statischem elektrischen Feld einzufangen. Die Idee der Paulfalle war es, hierfür ein rotierendes elektrisches Wechselfeld zu verwenden. Näheres unter https://de.wikipedia.org/wiki/Paul-Falle
xl https://www.aqt.eu/qc-systems/: Die Firma Alpine Quantum Technologies „AQT“ wurde aus der Zusammenarbeit der Universität Innsbruck und der Österreichischen Akademie der Wissenschaften gegründet. Offizielle Informationen zu dem 19“-Rack Quantencomputer, der aktuell nur Partnern zur Verfügung steht, gibt es noch nicht. AQT‘s Quantencomputer soll über die Python-Frameworks Qiskit, Cirq und Pennylane ferngesteuert werden können.
xli https://www.nist.gov/publications/demonstration-fundamental-universal-quantum-logic-gate: Wissenschaftliche Arbeit „Demonstration of a Fundamental Quantum Logic Gate“ von Christopher Monroe u.a. über die experimentelle Bestätigung von Cirac und Zollers CNOT-Gatter.
xlii https://www.youtube.com/watch?v=LRzhb7OkQ9s: Vortrag „Shaping the future of quantum computing“ vom Tony Uttley, dem Quantum Teamleader von Honeywell
xliii https://arxiv.org/abs/2003.01293: Wissenschaftliche Arbeit „Demonstration of the QCCD trapped-ion quantum computer architecture“ von Honeywells Team zum Hardwareansatz des eigenen Quantencomputers.
xliv https://en.wikipedia.org/wiki/Bernstein%E2%80%93Vazirani_algorithm: Wikipedia-Einführung für den Bernstein-Vazirani-Algorithmus
xlv https://en.wikipedia.org/wiki/Hidden_shift_problem: Kurze Erläuterung zum Hidden-Shift-Problem auf Wikipedia
xlvi https://www.youtube.com/watch?v=9aOLwjUZLm0: Sehr schöner Vortrag von Christopher Monroe über das Quantencomputing mit Ionenfallen-Quantencomputern. Ab Min. 0:22 erläutert er die Funktionsweise und die Vorteile von Ionenfallen-Quantencomputern. Am Ende des Videos geht er auch kurz auf das Startup „IonQ“ ein.
xlvii https://arxiv.org/abs/1208.0391: „Large Scale Modular Quantum Computer Architecture with Atomic Memory and Photonic Interconnects“: Gemeinsame Arbeit von Monroe und Kim, wie man mehrere Ionenfallen über Photonenkopplungen zu einem gro0en Ionenfallen-Quantencomputer skalieren könnte.
xlviii https://arxiv.org/abs/1903.08181: Wissenschaftliche Arbeit „Benchmarking an 11-qubit quantum computer“ von IonQs Team, in der sie Details zum Quantencomputer und zu den Benchmarks bekanntgeben.
xlix https://ionq.com/posts/december-09-2020-scaling-quantum-computer-roadmap: Hardware.Roadmap von IonQ
l https://en.wikipedia.org/wiki/Quadratic_unconstrained_binary_optimization: Definition eines QUBO-Problems auf Wikipedia. Allerdings sollte man sich davon nicht allzu sehr entmutigen lassen: QUBO-Probleme können tatsächlich auf viele Problem-Felder angewendet werden.
li Den Quantencomputer von D-Wave auf bloße Optimierungsaufgaben zu reduzieren wäre tatsächlich eine starke Untertreibung. Es zeigt sich nämlich, dass viele andere Aufgabengebiete in Optimierungsprobleme übersetzt werden können (u.a. im Maschine Learning, atomare Simulationen und selbst in abgewandelter Form die Primzahlzerlegung)-
lii https://arxiv.org/abs/1611.04471: wissenschaftliche Arbeit von T. Albash, D. A. Lidar „Adiabatic Quantum Computing“
liii https://de.wikipedia.org/wiki/Simulierte_Abk%C3%BChlung : Wikipedia-Beschreibung des Prinzips der simulierten Abkühlung
liv Dabei springt es bei diesem Vorgang nach und nach über alle lokalen Täler und findet irgendwann den höchsten Berg, also das globale Optimum. Aber ein Bild sagt mehr als 1000 Worte: Dieses Gif von Wikipedia sagt eigentlich schon alles aus.
Quelle: Kingpin13 / Wikipedia
lv Die Grundlage des Adiabatischen Prinzips ist bereits seit den Gründerzeiten der Quantenmechanik bekannt https://de.wikipedia.org/wiki/Adiabatisches_Theorem_der_Quantenmechanik: Sofern das eigentliche Problem (bzw. dessen „Hamilton-Operator“) langsam genug dazugeschaltet wird, verbleiben die Qubits die ganze Zeit im Grundzustand des Gesamtproblems. Dabei ist das Wort „Langsam“ der springende Punkt: Diese Zeit hängt vom Kehrwert der Differenz der Kostenfunktion des Grundzustandes und des ersten „angeregten“ Zustandes im Verlauf der Schaltung ab. Mit zunehmender Problem-Komplexität wird diese Differenz immer kleiner und die Schaltungszeit muss immer mehr verlängert werden. Schaltet man das Optimierungsproblem zu schnell dazu, springen die Qubits aus dem Grundzustand heraus.
lvi Dieser Satz von speziellen Quantenbausteinen wird auch „Ising-Modell“ genannt. Das Ising-Modell vereinfacht die Wechselwirkungen in komplexen Quantensystemen so geschickt, dass es in der theoretischen Physik gerne als vereinfachtes Modell für zu komplizierte Systeme verwendet wird (z.B. als Modell für den Ferromagnetismus).
lvii https://www.nature.com/articles/srep37107/figures/1: Jedes Qubit ist in einer Chimera-Zelle enthalten. Die benachbarten Zellen können miteinander verschaltet werden. Jede Chimera-Zelle besteht aus zwei 4er-Reihen von Qubits. Darin kann jedes Qubit einer Reihe mit jedem Qubit der Nachbarreihe verschaltet werden: Ein sogenannter „complete bipartite graph“. https://arxiv.org/abs/1508.05087: Durch den Fertigungsprozess können nur etwa 95% der Qubits wirklich verwendet werden. Im Anhang A wird dies im Detail sehr anschaulich dargestellt.
lviii Das Prinzip der Pegasus-Graphen wesentlich komplexer https://docs.dwavesys.com/docs/latest/c_gs_4.html#pegasus-graph. Die Qubits werden hier mehreren Gruppen zugeordnet die durch drei sich ergänzenden Kopplungsarten verschaltet sind.
lix https://www.dwavesys.com/take-leap: Das Cloud-Angbot von D-Wave.
lx https://docs.ocean.dwavesys.com/en/stable/getting_started.html: D-Waves Python-Framework „Ocean“. Hier finden Sie übrigens auch diverse Codebeispiele. Wie die anderen Frameworks der Konkurrenz wird „Ocean“ als OpenSource-Projekt auf Github gehostet.
lxii Termine und vergangene Konferenzen der „D-Wave Qubits“ googeln Sie am besten z.B. https://www.dwavesys.com/qubits-europe-2019
lxiii https://arxiv.org/abs/1708.01625: Wissenschaftliche Arbeit von Volkswagen (Team um Florian Neukart) und D-Wave „Traffic flow optimization using a quantum annealer“. Diese Arbeit war meines Wissens die erste über einen praktischen Usecase, der mit Hilfe eines Quantencomputers bearbeitet werden konnte. Auf der Websummit 2019 stellten sie hierzu ein überarbeitetes Verfahren im produktiven Einsatz vor https://arxiv.org/abs/2006.14162 / „Quantum Shuttle: Traffic Navigation with Quantum Computing“
lxiv https://www.scottaaronson.com/blog/?p=4794: Scott Aaronsons Blog-Beitrag über die wissenschaftliche Arbeit „The Power of Adiabatic Quantum Computation with No Sign Problem“ von Matt Hastings.
lxv https://arxiv.org/abs/1907.00707: wissenschaftliche Arbeit von Googles Quantum AI-Team „Quantum-Assisted Genetic Algorithm“, die Hinweise darauf gibt, dass für gewisse genetische Algorithmen das Quanten Annealing mit weniger Rechenschritten auskommen kann.
lxvi https://www.xanadu.ai: Homepage der kanadischen Firma Xanadu
lxvii https://arxiv.org/abs/1607.08535: „Why I am optimistic about the silicon-photonic route to quantum computing“, Artikel von Terry Rudolph
lxviii https://www.youtube.com/watch?v=Yi6jA-HDrEo : Vortrag „Unique architectures for photonic quantum computing“ von Naomi Nickerson über den Quantencomputer-Ansatz von PsiQuantum. https://www.youtube.com/watch?v=HEe53OE3HbU: Kurzer Vortrag von Jeremy O’Brien auf dem World Economic Forum.
lxix https://thequantumdaily.com/2020/04/07/psiquantum-quantum-computer-startup-raises-230-million-possibly-largest-qc-investment-to-date-2/: News-Meldung zu PsiQuantums rekordverdächtigen $215 Million-Fundraiser im Frühjahr 2020
lxx https://medium.com/xanaduai/a-day-in-the-life-of-xanadus-hardware-team-c19bab2b456d: Eine schöne Erläuterung von Xanadus-Team, was ein Phasenraum ist und wie ein Squeezed-State darin dargestellt wird.
lxxi https://en.wikipedia.org/wiki/Squeezed_coherent_state#Two-mode_squeezed_states: Hier die formularer Wikipedia-Beschreibung eines Two-Mode-Squeezed States, die Xanadu konkret verwendet.
lxxii https://www.youtube.com/watch?v=vF6PkXmo2XA: Vortrag „Scaling Photonic Quantum Computers“ von Zachary Vernon, Hardwarechef von Xanadu auf der virtuellen Konferenz Quantum For Business 2020. Sehr viel Information in 20 Minuten: In dem Vortrag gibt Vernon einen schönen Kompletten-Überblick über den aktuellen Stand, Hardwarepläne und Softwarelösungen von Xanadu.
lxxiii https://de.wikipedia.org/wiki/Mach-Zehnder-Interferometer: Wikipedia-Beschreibung eines Mach-Zehnder-Interferometers
lxxiv https://www.scottaaronson.com/blog/?p=1631: Blogbeitrag „BosonSampling Lecture Notes from Rio“ von Scott Aaronson einem der Erfinder des Boson Samplings. Die Links bieten eine umfassende Einführung in das Thema und erläutern u.a. warum Boson Sampling vermutlich mit keinem klassischen Computer effizient simuliert werden kann: Es zeigt sich nämlich, dass die Verteilungswahrscheinlichkeiten beim Boson Sampling mit einem schwer zu berechnenden mathematischen Objekt zusammenhängt: Die „Permanente“ einer Matrix.
lxxv https://arxiv.org/abs/1912.07634: Wissenschaftliche Arbeit „Applications of Near-Term Photonic Quantum Computers: Software and Algorithms“ von Xanadus Algorithms-Team
lxxvi https://arxiv.org/abs/1803.10730: Wissenschaftliche Arbeit „Using Gaussian Boson Sampling to Find Dense Subgraphs“ von Xanadus Algorithms-Team. „Graphen“ in Form von Knotenpunkten und Kanten, die diese Knoten verbinden, stellen ein beliebtes Hilfsmittel in der Mathematik und in den Computerwissenschaften dar. Mithilfe von Graphen lassen sich Beziehungen abbilden (z.B. verlinkte Internetseiten, in soziale Medien, …).
lxxvii https://strawberryfields.ai/photonics/index.html: Homepage von Xanadus Python-Framework „Strawberry Fields“ für das CV-Quantencomputing. Auf den sehr gut dokumentierten Folgeseiten wird teilweise auch die Hardware vorgestellt und in das CV-Quantencomputing im Allgemeinen eingeführt. Aber Hand aufs Herz: Auch wenn Xanadu sich dabei wirklich Mühe gibt, anders als für das Qubit-Quantencomputing benötigt man für das CV-Quantencomputing einiges an Grundlagen in Quantenmechanik und eigentlich auch in Quantenfeldtheorie (da man es hier mit beliebig vielen Teilchenzuständen zu tun hat).
lxxviii https://arxiv.org/abs/quant-ph/0008040: Wissenschaftliche Arbeit „Encoding a qubit in an oscillator“ von den „Godfathern“ der Quantenfehlerkorrektur Gottesmann, Kitaev und Preskill um CV-Quantencomputer in Quantencomputer mit fehlerkorrigierten Qubits zu überführen.
lxxix https://medium.com/xanaduai/from-a-state-of-light-to-state-of-the-art-the-photonic-path-to-millions-of-qubits-c0e08ca1cb21: Artikel „Riding bosonic qubits towards fault-tolerant quantum computation“ von Xanadu, in dem das Prinzip von GKP-Zuständen anschaulich erklärt wird.
lxxx https://arxiv.org/abs/2010.02905: Wissenschaftliche Arbeit „Blueprint for a Scalable Photonic Fault-Tolerant Quantum Computer“ in der Xanadu den Architekturansatz für einen fehlerkorrigierten Quantencomputer vorstellt. Der Text ist allerdings schwer verdaulich. Als Einstieg empfehle ich eher den folgenden Artikel:
lxxxi https://medium.com/xanaduai/riding-bosonic-qubits-towards-fault-tolerant-quantum-computation-95b92c78cb43: Artikel „From a state of light to state of the art: the photonic path to millions of qubits“ von Xanadus Team, der die Grundaussagen aus dem Paper wesentlich leichter verdaulicher erklärt.
lxxxii https://www.techrepublic.com/article/alibaba-puts-quantum-computing-in-the-public-cloud-follows-intel-and-ibms-lead,
lxxxiii http://quantumcomputer.ac.cn/index.html: Mittlerweile zeit das damalige Cloud-Angebotvon Alibaba nur noch Schriftzeichen an.
lxxxiv https://arxiv.org/abs/2005.06787: Wissenschaftliche Arbeit „Classical Simulation of Quantum Supremacy Circuits“ von Alibabas Quantum Team über ein verbessertes Simulationsverfahren für Quanten-Schaltkreise auf herkömmlichen Computern.
lxxxv https://science.sciencemag.org/content/370/6523/1460: Chinas wissenschaftliche Veröffentlichung „Quantum computational advantage using photons“ in der Fachzeitschrift „Science“. Und hier der öffentlich zugängliche Link zu der Vorveröffentlichung derselben Arbeit auf arxiv.org https://arxiv.org/abs/2009.01177: „Benchmarking 50-Photon Gaussian Boson Sampling on the Sunway TaihuLight“. Wie bei allen Hardware-Veröffentlichungen muss man schon ziemlich tief in der Thematik drinstecken, um dem Artikel zu folgen. Aber man bekommt einen Eindruck, wie ungeheur komplex die Herausforderung ist (und die einführenden Passagen sind auf jeden Fall lesenswert)
lxxxvi Wie die astronomisch hohe Zahl zustande kommt, kann man sich leicht klar machen. Versucht man N Tennisbälle in M Körbe zu verteilen merkt man: Mit jedem weiteren Korb vervielfacht sich die bisherige Anzahl die Bälle in die Körbe zu verteilen, also eine exponentielle Steigerung.
lxxxvii Um die Häufigkeitsverteilung vom Boson-Sampling zu berechnen, muss man die „Permanente einer unitären Matrix“ berechnen. Letztere wird exponentiell groß. Aaronson und Arkhipov wussten, dass diese Aufgabe keinen effizienten klassischen Algorithmus besitzen kann, weil dies am Ende allgemein vermuteten Gesetzmäßigkeiten der Komplexitätstheorie widersprechen würde. Falls Sie sich das Thema genau ansehen wollen empfehle ich Ihnen https://www.scottaaronson.com/blog/?p=1631: Scott Aaronsons Übersichtsseite „BosonSampling Lecture Notes from Rio“. Die Links bieten eine umfassende Einführung in das Thema und erläutern u.a. warum Boson Sampling vermutlich mit keinem klassischen Computer effizient simuliert werden kann. Hier erfahren Sie auch Details über das „Gaussian Boson Sampling“, die Ausprägung, die von den chinesischen Forschern verwendet wurde. Dass das Boson Sampling ein super-effizienter Weg ist, um die Permanente einer unitären Matrix zu berechnen, ist auch der Grund für seine Anwendungen: Das Dense-Sub-Graph-Problem lässt sich nämlich z.B. ebenfalls auf die Permanente einer unitären Matrix umwandeln.
lxxxviii https://www.spektrum.de/news/ich-bin-froh-ueber-meine-rueckkehr-nach-china/1526607: Interview von der Spektrum-Redaktion mit Jian-Wei Pan im Jahr 2017.
lxxxix https://www.scottaaronson.com/blog/?p=5159: Scott Aaronsons sehr detaillierter Blogeintrag „Chinese BosonSampling experiment: the gloves are off“. Am Betrag und an dessen Kommentarbereich bekommen Sie unter anderem einen Eindruck davon, wie der Puls der Forschung in Echtzeit funktioniert. Unter anderem erläutert Aaronson auch, dass der Photon-Loss von 70%, der bei dem Experiment gemessen wurde, eine Simulation durch einen klassischen Rechner eventuell möglich machen könnte. Außerdem erläutert er, dass man ähnliches bei Googles Experiment mit Sicherheit ausschließen kann, weil dort mit dem „Linear Cross-Entropy“ ein Verfahren existiert, über das man sicherstellen kann, ab wann die gemessenen Ergebnisse klassisch nicht reproduzierbar sind.
xc Die topologischen Quantencomputer wurden im Jahr 1997 von dem theoretischen Physiker Alexei Kitaev vorgeschlagen, der auch bereits zuvor den zentralen Algorithmus für die Quantenfehlerkorrektur entdeckt hatte. Sie ahnen es wohl: Ein topologischer Quantencomputer hat quasi eine eingebaute Quanten-Fehlerkorrektur. Das Herzstück der topologischen Quantencomputer sind sogenannte „Majorana-Quasiteilchen“, mit denen man ein einzelnes Qubit räumlich in die Länge ausdehnen kann. Die Quanteninformation in einem Qubit ist damit nicht mehr in einem einzelnen Punkt im Raum lokalisiert und kann nur noch über koordinierte Aktionen auf ganze Raumbereiche verändert oder ausgelesen werden. Das ganze Konzept der topologischen Quantencomputer ist so neu, dass die ersten Hinweise für Majorana-Quasiteilchen vor gerade mal zehn Jahren gefunden wurden. Näheres erfahren Sie hier https://www.nature.com/news/inside-microsoft-s-quest-for-a-topological-quantum-computer-1.20774 und in https://arxiv.org/abs/1501.02813: „Majorana Zero Modes and Topological Quantum Computation“, Fachartikel von Michael Freedman et al.
xci https://www.wired.com/story/microsoft-win-quantum-computing-error/: Der sehr detaillierte Artikel „Microsoft’s Big Win in Quantum Computing Was an ‘Error’ After All“ über Microsofts Ambitionen und über den herben Rückschlag des Projektes. Anscheinend wurden Daten die 2018 zur Meldung eines Durchbruchs führten „fehlinterpretiert“ bzw. die Daten, die nicht passten, wurden in der Analyse weggelassen.
xcii https://docs.microsoft.com/en-us/azure/quantum/overview-azure-quantum: Überblick, einige Quick-Start-Beispiele für die verschiedenen Azure-Quantum-Dienste und eine komplette Referenzdokumentation für das Quantum Development Kit QDK von Microsoft.