Kategorie: Qubit

In diesem Beitrag erfahren Sie die grundlegenden Eigenschaften eines einzelnen Qubits und der Quantengatter. Da das Qubit das einfachste Quantensystem ist, lernen Sie dabei auch viel über die Quantenmechanik. Danach werden Sie verstehen warum die Quantenwelt und mit ihr die Qubits und die Quantenprogrammierung so faszinierend ist.

Dabei verwende ich keine „Höhere Mathematik“. Ich versuche Ihnen aber das Wesen der Gleichungen bildlich zu erklären. Damit werden Sie in der Lage sein selbst einen Eindruck davon zu bekommen was Physiker meinen, wenn sie z.B. sagen „Das Elektron ist sowohl Teilchen als auch Welle“.

Ein Magier bei „Britain Has Got Talent“

Fountain Studios, London, 26.5.2014:

Der 25 jährige Kanadier Darcy Oake betritt die Bühne der beliebten Talent-Show „Britain‘s Got Talent“. Was er im Begriff ist zu zeigen wird die Jury und sämtliche Zuschauer buchstäblich aus den Socken hauen.

In der Mitte der Bühne steht ein Gerüst mit einem Podest. Darcy Oake steigt auf eine Stahltreppe nach oben. Dort angekomment erklärt er dem Publikum, was wir schon vermuten: Von diesem Podest wird er nun verschwinden. Der Clou dabei ist Folgendes: dabei zeigt er auf einen Mann, der eine große Kamera geschultert hat und langsam über die Bühne wandert .Alles wird aus verschiedenen Blickwinkeln mitgefilmt und auf einer großen Leinwand live gezeigt.

Es geht los. Während der Kameramann um das Podest wandert sehen wir das Videobild von Darcy Oake, der sich auf dem Podest auf einen Stuhl setzt und sich ein riesiges Tuch über seinen Kopf zieht. Der Kameramann läuft auf der Bühne um das Gerüst herum. Kein Trick ist erkennbar. Wir sehen nur das flatternde Tuch und darunter die Männergestalt von Darcy Oake. Plötzlich fällt das Tuch auf dem Podest zu Boden und Darcy Oake ist … natürlich verschwunden. Aber jetzt kommt das Unglaubliche: Ein Assistent geht hinüber zum Kameramann, der immer noch mitten auf der Bühne steht. Der Assistent nimmt ihm die große Kamera aus den Händen und dreht sie herum. Jetzt sehen wir das Gesicht des Kameramannes auf der Leinwand. Es ist … Darcy Oake. Unglaublich.

Sie sollten sich selbst ein Bild davon machen. Der Trick und auch die Reaktion der Jury darauf sind einfach sehr cool. Hier geht’s zum Video:

https://www.youtube.com/watch?v=C5N0MDF1CYQ

Was ich so faszinierend an dem Trick finde: Für eine kurze Zeitspanne hat es Darcy Oake so aussehen lassen, als wäre er zweimal gleichzeitig vorhanden gewesen auf der Bühne: Ein Ich als Zauberer auf dem Podest und ein zweites Ich als Kameramann neben dem Podest. Erst als der Assistent das Geheimnis lüftet, wird allen Zuschauern klar, wer er jetzt ist.

Es gibt noch einen anderen Grund, warum ich den Trick so wunderbar finde: Was ich gerade beschrieben habe ist genau das was ein Qubit in der Quantenwelt ausmacht. Darcy Oake verhält sich in seinem Trick also genauso wie ein Qubit.

Warum meine ich das?

Das Qubit

Ein Qubit ist die einfachste Zustandsform der Quantenphysik. Ein binärer Quantenzustand der genau zwei Zustände besitzt. Meistens werden sie mit 0 und 1 bezeichnet, manchmal als „up“ und „down“, es ist ganz egal. Soweit unterscheidet sich ein Qubit nicht von einem Bit in einem herkömmlichen Computer ist. Letzteres ist ein elektronischer Schalter, der zwei Werte haben kann: An oder aus. Dies wird normalerweise durch die Zahlen 1 und 0 symbolisiert. Das Bit hat also entweder den Wert 1 oder den Wert 0.

Und das ist genau der Unterschied und das Unerklärbare an einem Qubit. Genau wie Darcy Oake in seinem Zaubertrick nimmt das Qubit beide „Ich-Zustände“ gleichzeitig ein. Im Laufe der Zeit „pendelt“ das Qubit bildlich gesprochen zwischen diesen Zuständen hin und her: Mal ist es mehr 1, mal ist es mehr 0. Und damit meine ich nicht, dass das Qubit z.B. mal den Wert 0.321, also näher bei 0, und mal den Wert 0,7681, also näher bei 1, hat. Nein: Es gibt wirklich nur die Werte 0 und 1, und beide in einer gemischten oder auch überlagerten Form.

Diese überlagerte Form lässt sich vereinfacht mit einem Zeiger auf einer Kreislinie vergleichen, wie ich es in dem Diagramm unten aufgezeichnet habe. Der Qubit-Zeiger pendelt entlang der Kreislinie. Die zwei gleichzeitig vorhandenen Ich-Zustände sind die x-Achse und die y-Achse des Diagramms. Die aktuellen x- und die y-Werte der Zeigerspitze (also die Ordinate und die Abszisse) sind ein Maß für die Wahrscheinlichkeit in diesem Moment den Zustand zu messen.

Die Stellung der Achsen „Kameramann“ und „Zauberer auf dem Podest“ haben übrigens nichts mit den tatsächlichen Positionen auf der Bühne zu tun. Das vereinfachte Zeigerbild zeigt an, welche Überlagerung das Qubit in einem abstrakten Parameterraum besitzt. Nebenbei: Diese spezielle Art von Raum wird „Hilbertraum“ genannt, benannt nach dem deutschen Mathematiker David Hilbert, dem vielleicht wichtigsten Mathematiker des 20. Jahrhunderts ⁱ.

Natürlich gibt es in der Quantenphysik für das Qubit eine exakte mathematische Beschreibung. Die am Anfang ungewöhnliche Schreibweise lautet:

|qubit⟩ = 0.500 * |0⟩ + 0.866 * |1⟩

Die Schreibweise mit den |0⟩ und |1⟩ soll klar machen, dass es sich hierbei nicht um Zahlen, sondern um Zustände, also Objekte handelt. Wir hätten auch schreiben können |Kameramann⟩ für |0⟩ und |Zauberer auf dem Podest⟩ für |1⟩.

Nur die roten Dinger vor den Zuständen sind echte Zahlen. Die Zahlen sind ein Maß dafür, wie wahrscheinlich im Moment der Zustand |0⟩ oder |1⟩ gemessen werden würde. Im Laufe der Zeit, also während der Pendelbewegung, verändern sich die Zahlen nach einem genau bekannten Gesetz, der sogenannten „Schrödingergleichung“. Während eines Quantenprogramms werden diese roten Zahlen durch einen festen Satz von Quantengattern, den Grundbausteinen der Quantenprogramme verändert.

Wenn Sie genau hinsehen, bemerken Sie, dass die „Wahrscheinlichkeiten“ 0.500 und 0.866 nicht zusammen 1 ergeben (was in der normalen Wahrscheinlichkeitsrechnung 100% entsprechen würde). Der Grund: An der Gleichung oben gibt es ein paar mathematische Gemeinheiten, die die Sache noch einiges ungewöhnlicher machen ⁱⁱ. Das exakte Zeigerbild für ein Qubit werde ich in einem späteren Beitrag beschreiben ⁱⁱⁱ. Für die Themen, die ich in diesem Beitrag beschreibe, reicht die vereinfachte Sichtweise aber schon ganz gut aus.

Nehmen wir als Beispiel ein Qubit, das im Zustand |0⟩ beginnt und dann in den Zustand |1⟩ übergeht.

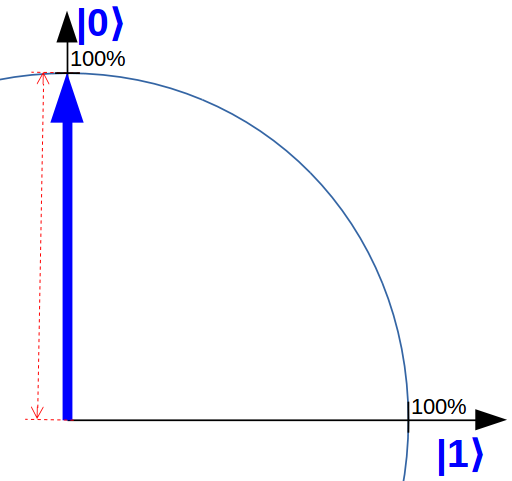
|qubit⟩ = |0⟩

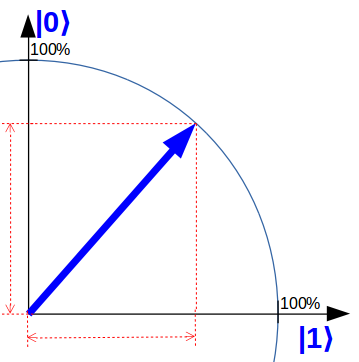
|qubit⟩ = 0.707 * |0⟩ + 0.707 * |1⟩

 

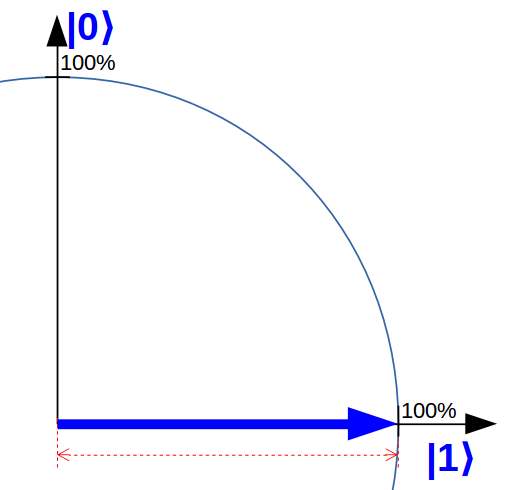|qubit⟩ = |1⟩

Die „Pendelbewegung“ geht solange weiter, bis wir das Qubit tatsächlich messen und es in Interaktion mit seiner Umgebung treten muss. In diesem Moment entscheidet sich das Qubit für einen der beiden Ich-Zustände. Und zwar entscheidet es sich um so mehr für den Zustand, in dessen Richtung das Pendel vorher ausgeschlagen hat.

Dieses Verhalten des Qubits mag vielleicht auf den ersten Blick zwar etwas verwirrend aber doch irgendwie banal aus. Tatsächlich ist dieses Verhalten aber absolut unglaublich. Dieses Verhalten eines Qubits, und natürlich auch jedes anderen Quantenzustandes, ist einer der Gründe warum die Quantenwelt auch über 100 Jahren nach ihrer Entdeckung vielleicht das größte Rätsel der Naturwissenschaften ist:

Es ist als würde die Natur in ihren kleinsten, atomaren Strukturen Darcy Oakes Magie mit den beiden Ich-Zuständen ausführen, die gleichzeitig auf der Bühne sind.

Allerdings nicht als Trick, sondern in echt.

Der „Welle-Teilchen-Dualismus“

Was ich gerade beschrieben habe nennt man auch den „Welle-Teilchen-Dualismus“ der Quantenmechanik: Ein Qubit nimmt mehrere Zustände gleichzeitig ein, wie eine Welle. Bei jeder Messung, die wir durchführen, verhält es sich aber wie ein normales Teilchen und wir messen nur noch einen einzigen Zustand.

Die Sache mit der Welle kommt so ins Spiel: Ein Qubit besitzt nur zwei Zustände. Normalerweise besitzt ein Quantenobjekt wesentlich mehr Zustände und oft sogar unendlich viele! Für ein Elektron sind dies z.B. die Orte sein, an dem es sich aufhalten kann. Unser vereinfachtes Zeigerbild passt dann trotzdem noch. Nur besitzt das Diagramm dann nicht mehr nur zwei Achsen, sondern eine Achse für jeden möglichen Zustand. Also sehr sehr viele Achsen, die senkrecht aufeinander stehen. Gegebenenfalls auch unendlich viele Achsen. Natürlich kann man sich das nicht mehr vorstellen, weil wir uns nur einen Zeiger in einem Diagramm mit höchstens drei Achsen vorstellen können. In der Mathematik kann man solche Systeme mit unendlich vielen Dimensionen trotzdem exakt berechnen. Dieser Zweig der Mathematik wird „Funktionalanalysis“ genannt ^iv. Den Zeiger können wir dann immer noch auf die gleiche Weise schreiben. Jetzt allerdings mit mehr Zuständen.

|elektron⟩ = 0.0134 * |Ort 1⟩ + 0.0136 * |Ort 2⟩ + 0.0137 * |Ort 3⟩ + 0.0137 * |Ort 4⟩ +

….

+ 0.0317 * |Ort 10000⟩ + 0.0316 * |Ort 10001⟩ + 0.0315 * |Ort 10002⟩ +

….

Daraus können wir uns jetzt unsere Welle zusammenbauen: Dazu reihen wir blauen Orts-Zustände wie eine Perlenschnur in der x-Achse aneinander. Die roten Wahrscheinlichkeits-Zahlen zeichnen wir als Pendelausschlag an diesem Ort auf der y-Achse ein. Heraus bekommen wir gerade das Bild einer Welle.

Das sollte Sie aber nicht in die Irre führen. Das Elektron ist keine Welle. Das Elektron ist wie dieser blaue Zeiger in einem Diagramm, dessen Zeigerspitze immer an einer bestimmten Stelle in dem abstrakten Hilbertraum mit den vielen senkrechten Achsen steht. Nur die Wahrscheinlichkeiten kann man so darstellen, dass sie aussehen wie eine Welle.

Der „Welle-Teilchen-Dualismus“ hat für Elektronen erstaunliche Konsequenzen: Es gibt dieses berühmte „Doppelspalt-Experiment“ in dem ein einzelnes Elektron durch zwei benachbarte Spalte gleichzeitig fliegt und auf eine Art Leinwand trifft. Dort heben sich die Wahrscheinlichkeiten komplett auf oder verstärken sich. Das Elektron „interferiert“ also mit sich selbst ^v.

Der abstrakte Hilbertraum hat übrigens die interessante Eigenschaft, dass er die Entfernungsinformationen der Orte komplett auflöst: Im Hilbertraum stehen alle Ortszustände als eigene Achse senkrecht aufeinander. Die Zeigerspitze ist von jedem Ort „gleichweit entfernt“. Nämlich höchstens um eine 90°-Drehung. Oder anders ausgedrückt: Um von hier bis ins Sternbild Alpha Centauri zu springen, muss das Elektron im Hilbertraum nur eine 90°-Drehung durchführen. Das gleiche gilt für einen Mikro-Sprung von einem Atom zum nächsten.

Ich finde das faszinierend. Vielleicht ist genau das, die richtige Sicht auf unser Universum und unsere Vorstellung von Entfernung kommt nur durch Nebeneffekte zustande ^vi.

Die Grundidee eines Quantenprogramms

Jetzt werden Sie vielleicht sagen: Moment mal, die Argumentation ist zu dämlich! Das Qubit soll zwei Ich-Zustände zugleich einnehmen, obwohl das eigentlich unmöglich ist. Und wenn wir versuchen genau das zu beobachten, verschwindet der Effekt wieder. Wer soll das denn glauben ?!

Nun ja, viele Physiker wollten das am Anfang auch nicht glauben. Aber viele Experimente haben nachgewiesen, dass in der kurzen unbeobachteten Zeitspanne zwischen zwei Messungen, etwas ungeheuer Merkwürdiges passieren muss, das sich nur durch diese Art von Ich-Überlagerung erklären lässt.

Und dieses ungeheuer Merkwürdiges kann genutzt werden, um neue Arten von Berechnungen auszuführen:

Nehmen wir nochmal das Zauberer-Beispiel. Angenommen Darcy Oake muss eine Aufgabe lösen, die er niemals alleine lösen könnte. Zum Beispiel soll er die Rechenaufgabe 16 – 7 nur mit seinen Fingern lösen. Nur mal angenommen ihm geht es so, wie meinem kleinen Sohn und er kann sie wirklich nicht anders lösen als die Zahlen mit seinen 10 Fingern abzuzählen. Da die Aufgabe aber mit einer Zahl größer als 10 zu tun hat, ist sie für ihn eigentlich nicht lösbar. Jetzt startet er einfach seinen Trick. Er zaubert sein zweites Ich auf die Bühne. Zusammen lösen sie die Aufgabe mit ihren vier Händen. Am Ende zeigen jeweils beide Ichs die Zahl 9 mit Fingern in die Luft. Jetzt ist es egal welches der beiden Ich-Zustände von Darcy Oake am Ende gemessen wird und übrig bleibt. Er hat also die „unmögliche“ Aufgabe gelöst.

Das ist natürlich ein blödes Beispiel. Aber ich hoffe, Sie verstehen worauf ich hinaus will. Natürlich hat ein Qubit keine Finger. Für ein einzelnes Qubits muss man eher eine Frage stellen, die mit Ja oder Nein beantwortet werden kann. Ausserdem sind die beiden Ich-Zustände eines einzelnen Qubits nicht unabhängig voneinander, wie Sie am Zeigerbild oben sehen können. Richtig rechnen kann man erst mit mehreren Qubits.

Das bringt uns sofort zu der Frage: Wie könnte man denn mit einem Qubit rechnen?

Dafür muss man verstehen, wie man ein Qubit überhaupt verändern kann. Das führt uns direkt zu den „Quantengattern“ für Quantencomputer. Im Detail erfahren Sie das in den nächsten Beiträgen auf Quantencomputer-Info. Wenn Sie ausschließlich an der Quantenprogrammierung interessiert sind, können Sie den Rest dieses Beitrags also überspringen. Im Rest dieses Beitrages bekommen Sie von mir ein paar Erläuterungen und Hintergründe zu den Quantengattern, die Ihnen dabei helfen sollten ein besseres Verständnis dafür zu entwickeln.

Der Elektronen-Spin: Die Mutter aller Qubits

Um die Unregelmäßigkeiten in Strahlungs-Experimenten von Atomhüllen zu erklären, schlugen mehrere Physiker Ende der 1920er Jahren vor, dass jedes Elektron einen inneren Drall besitzen müsste: Der Elektronen-Spin. Der Eigendrall dieses Spins dürfte nur zwei mögliche Werte besitzen: „Wert ½, die Drehachse zeigt nach oben“ oder „Wert -½, die Drehachse zeigt nach unten“. Anders ausgedrückt: |up⟩ oder |down⟩ oder noch einfacher: |0⟩ oder |1⟩ . Der Elektronen-Spin ist als das allererste qubit-artige System in der Quantenmechanik.

Der österreichische Physiker Wolfgang Pauli untersuchte daraufhin die quantenmechanischen Gesetze nach denen sich das Spin-Qubit verändern kann. Die Grundbausteine, die er dafür fand wurden deshalb nach ihm benannt: „Die Paulimatrizen“. Alle anderen Qubits gehorchen auch den Paulimatrizen. Die Spin-Qubits haben aber die interessante Eigenschaft, dass sie eine Raumrichtungen auszeichnen, nämlich der Drehachse des Eigendralls. Und deshalb lassen sich die Paulimatrizen für Spin-Qubits, sehr schön anschaulich beschreiben.

Im Zentrum steht unter anderem die Frage: Wie dreht sich ein Spin-Qubit im Raum? Sie werden sehen, die Antwort ist absolut erstaunlich!

Wie dreht sich ein Spin-Qubit im Raum?

Nehmen wir erst mal einen ganz normalen Gegenstand. Angenommen Sie sitzen einem Bürostuhl gegenüber. Wenn Sie den Bürostuhl drehen scheint es so als ob er seine Form verändert. Natürlich macht er das nicht. Er sieht einfach aus jeder Blickrichtung anders aus. Dabei kommt es noch darauf an um welche Achse Sie den Bürostuhl drehen: Wenn Sie der Sitzfläche eine halbe Umdrehung versetzen sehen Sie die Rückseite des Bürostuhls. Wenn Sie die halbe Umdrehung anders durchführen, z.B. indem Sie ihn kopfüber drehen, sehen Sie auch die Rückseite. Allerdings ist der Bürostuhl jetzt auch noch auf den Kopf gestellt.

Gilt das gleiche für ein Spin-Qubit? Sieht es aus jeder Blickrichtung anders aus, je nachdem wie wir es drehen?

Ja, es sieht aus jeder Blickrichtung anders aus.

Bevor ich das genauer erkläre, müssen wir das Beispiel vom Zauberer und der Bühne noch etwas verfeinern.

Ich hatte Ihnen im vorangegangenen Abschnitt erklärt, dass ein Qubit ein Quantenzustand aus zwei überlagerten Zuständen ist, die es auf geheimnisvolle Weise beide gleichzeitig einnimmt. Im Zauberer Beispiel waren das die beiden Ich-Zustände „Kameramann“ und „Zauberer auf dem Podest“, die auf magische Weise gleichzeitig auf der Bühne vorhanden waren. Wir können uns das Qubit als gedankliches Pendel vorstellen, dass zwischen diesen beiden Ich-Zuständen hin- und herpendelt. Je mehr das Pendel in die Richtung eines Ich-Zustandes ausschlägt, um so wahrscheinlicher wird dieser Ich-Zustand am Ende gemessen. Vor der Messung sind trotzdem beide Ich-Zustände gleichzeitig vorhanden. In unserem Beispiel vom Zauber könnten wir uns diese Wahrscheinlichkeiten so vorstellen: Je unwahrscheinlich z.B. der Zustand „Kameramann“ wird, um so durchsichtiger wird er. Ist der Kameramann komplett ausgeblendet, ist die Wahrscheinlichkeit den Zustand „Kameramann“ zumessen gleich Null Prozent. Ist er vollkommen eingeblendet messen wir den Kameramann mit 100%-iger Wahrscheinlichkeit. Dazwischen sind alle Wahrscheinlichkeitswerte erlaubt. Wir wollen uns die Wahrscheinlichkeiten für die Ich-Zustände also so vorstellen, als wären wir ein Videotricktechniker, der an einem Ein-/Ausblende-Regler für Darcy Oake herumspielt. An dem Zeigerbild oben erkennen wir außerdem: Wenn wir den Zustand „Kameramann“ langsam ausblenden, blenden wir den Zustand „Zauberer auf dem Podest“ automatisch ein.

Ist der Zeiger um 45° gedreht sind der „Kameramann“ und der „Zauberer auf dem Podest“ gleich stark eingeblendet. Es gibt ein haufig benutztes Quantengattern, dass sich vereinfacht betrachtet ganz ähnlich verhält. Das „Hadamard“-Quantengatter oder einfach „H“. Was ich gerade bildlich beschrieben habe schreibt man in der Quantenmechanik:

H |0⟩ = 0.707 * |0⟩ + 0.707 * |1⟩

Das Hadamard-Quantengatter ist ein sehr oft verwendeter Baustein in Quantenprogammen. Wenn man es z. B. auf alle Qubits in einem Quantencomputer anwendet, belegt es den Speicher in dem Quantencomputer mit allen verfügbaren Werten gleichzeitig.

Das X-Quantengatter: Die Drehung auf der Bühne

Jetzt zur Drehung im Raum.

Das vertrakte dahinter ist, dass das Zeigerbild unseres Qubits nur zwei Achsen besitzt. Der Raum hat aber drei Dimensionen. Tatsächlich steckt dahinter ein altes mathematisches Rätsel: Wie kann ich einen Zeiger mit zwei Komponenten verändern, so dass diese Transformation eine Drehung im Raum darstellt. Das ist knifflig, weil das Ganze eindeutig sein muss. An der Veränderung des Zeigers muss ich eindeutig ablesen können, wie das Qubit im Raum gedreht wurde. Andersherum muss eine bestimmte Drehung im Raum den das Qubit immer auf dieselbe Art und Weise ändern. Das Ganze muss zumindest für kleine Drehungen gelten. Ein Teilgebiet der Mathematik beschäftigt sich mit solchen Fragen: Die „Darstellungstheorie“. Das Problem wurde tatsächlich 50 Jahre vor der Entdeckung der Quantenmechanik von dem Mathematiker William Clifford gelöst. Die endgültige Lösung für das Problem werde ich erst im nächsten Beitrag vorstellen. Unser Beispiel mit dem vereinfachten Zeigerbild können wir aber jetzt schon verwenden, um einen besseren Eindruck von den Quantengattern H, X, Y und Z zu bekommen. Später werden wir dieses Bild dann verfeinern.

Nehmen wir zwei Assistenten, die auf der linken Seite der Bühne stehen und sich den Zaubertrick zunächst nur anschauen. Beide stehen am Anfang nebeneinander. Nehmen wir als Beispiel an, das dass der Zeiger des Kameramann – Zauberer auf dem Podest – Qubits am Anfang auf „Zauberer auf dem Podest“ steht. D.h. er ist komplett sichtbar und der Kameramann ist komplett unsichtbar.

Jetzt geht der erste Assistent langsam gegen den Uhrzeigersinn vorne um die Bühne herum. Während er läuft sieht er, dass der Kameramann langsam sichtbar und der Zauberer im Kasten immer mehr ausgeblendet wird. Für ihn ist es, als würde durch sein Laufen ein magischer Schieberegler verschoben, der beide Zauberergestalten videotechnisch ein- und ausblendet.

Der erste Assistent ist jetzt so weit gegangen, dass er vorne auf der Bühne und direkt vor dem Zauberer-Qubit steht. Der zweite Assistent steht immer noch links neben dem Qubit. Der gelaufene Assistent sieht Folgendes: Der Kameramann ist jetzt genauso eingeblendet, wie der Zauberer auf dem Podest und letzterer ist also entsprechend ausgeblendet. Wenn Sie sich an das Beispiel mit dem 45°-Winkel erinnern, werden Sie erkennen, dass der erste Assistent durch sein Laufen also ein Hadamard-Quantengatter auf das Qubit ausgeführt hat.

Jetzt geht der erste Assistent langsam weiter gegen den Uhrzeigersinn vorne um die Bühne herum. Der Kameramann wird weiter eingeblendet, während der Zauberer auf dem Podest weiter ausgeblendet wird. Als er auf der anderen Seite der Bühne, der rechten Seite, angekommen ist stoppt er. Was sieht er jetzt? Der Kameramann ist komplett eingeblendet und der Zauberer auf dem Podest ist komplett ausgeblendet. Wenn er jetzt das Zauberer-Qubit messen würde, würde er immer den Kameramann messen.

Aber was sieht der zweite Assistent, der die ganze Zeit auf der linken Seite der Bühne stehengeblieben ist? Für ihn hat sich die ganze Zeit nichts geändert: Nur der Zauberer auf dem Podest ist zu sehen und der Kameramann ist komplett unsichtbar. Wenn der zweite Assistent also das Zauberer-Qubit messen würde, würde er immer den Zauberer auf dem Podest messen. Also genau das Gegenteil von dem ersten Assistenten.

So sieht also ein Qubit aus den verschiedenen Blickrichtungen aus.

Die Drehung um 180° auf der Bühne hat übrigens auch einen festen Namen: X-Quantengatter. Also ein weiterer Baustein der Quantenlogik.

Was ich gerade bildlich beschrieben habe schreibt man in der Quantenmechanik:

X |0⟩ = |1⟩ und X |1⟩ = |0⟩

Das X- Quantengatter in einem Quantencomputer ist also das Gegenstück zu einem NICHT-Gatter in einem herkömmlichen Computer: Es kehrt jeden Zustand in sein Gegenteil um.

Wenn wir das X- Quantengatter mit einem Hadamard-Quantengatter wie oben kombinieren bekommen wir:

X * H |0⟩ = X* ( 0.707 * |0⟩ + 0.707 * |1⟩ )

= X * 0.707 |0⟩ + X * 0.707 |1⟩

= 0.707 * X |0⟩ + 0.707 * X |1⟩

= 0.707 * |1⟩ + 0.707 * |0⟩

Die Quantengatter verändern also nur die blauen Zustände und nicht die roten Zahlen. Das Gleiche gilt für das Plus-Zeichen. Haben Sie die Rechnung verstanden? Herzlichen Glückwunsch! So sehen die Rechnungen in der Quantenmechanik aus (meistens allerdings ein bisschen komplexer). An dieser kleinen Rechnung können Sie übrigens auch schon verstehen, wieso es den Quantenparallelismus gibt. Warum erkläre ich Ihnen gleich im Anschluss.

In der Quantencomputer-Programmierung verwendet man für solche Rechnungen üblicherweise auch Quanten-Schaltungsdiagramme:

 

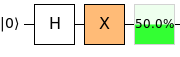
Die 50%-Anzeige ist kein zusätzliches Quantengatter und soll nur verdeutlichen, dass am Ende beide Zustände |0⟩ und |1⟩ mit gleicher Wahrscheinlichkeit gemessen werden würden.

Der Grund für den Quantenparallelismus

Wir haben gerade gesehen, dass die beiden Quantengatter X und H nur die blauen Qubit-Zustände verändern und die einfachen roten Zahlen übersehen. Sie übersehen auch das Plus-Zeichen dazwischen. Das ist eine Eigenschaft die alle Operationen der Quantenmechanik und somit auch alle Quantengatter besitzen. In unserer Erfahrungswelt sind wir auf die Messungen der Quanten-Systeme angewiesen und zerstören dabei die Überlagerungen der Qubit-Zustände. Ein Quantengatter hat im Gegensatz dazu kein Problem mit den Überlagerungen. Es wirkt auf jeden blauen Qubit-Zustand gleichberechtigt und erhält dabei die Überlagerung (in Form von den roten Zahlen und dem Plus-Zeichen). Ein X-Quantengatter führt z.B. in einem Rechenschritt parallel zwei NICHT-Operationen aus. Dafür müssen wir nichts tun. Die Quantenmechanik leistet das für uns umsonst. Diese Tatsache steckt hinter dem Quantenparallelismus.

Die beschriebene Eigenschaft der Quantengatter nennt man in der Mathematik übrigens „Linearität“. Die algebraischen Berechnungen die man auf diese Weise durchführt nennt man entsprechend „Lineare Algebra“.

Die Geburtstunde der Quantenmenchanik und die „Heisenbergsche Unschärferelation“

Ich hoffe, Sie haben noch etwas Luft für den Rest des Beitrages. An dieser Stelle kann ich es mir nicht verkneifen, noch die Mutter aller Quantenphänome kurz vorzustellen (obwohl dies eher weniger mit Quantencomputern zu tun hat). Über wohl keine Eigenschaft der Quantenmechanik wurde soviel geschrieben und philosophiert wie über die „Heisenbergsche Unschärferelation“. Kommen wir also zur Geburtsstunde der Quantenmechanik:

Helgoland, 1925: Der junge Göttinger Physiker Werner Heisenberg nimmt sich mehrere Wochen Urlaub, um seinen Heuschnupfen auf der Insel Helgoland zu kurieren. Die Wochen wird er nutzen um die offenen Rätsel der Atomphysik zu untersuchen. Im Juni gelingt ihn der Durchbruch und er schreibt einen Aufsatz, der die Wissenschaft revolutionieren wird. Seine neue Theorie, die „Quantenmechanik“ erklärt das Verhalten von Objekten im atomaren Maßstab auf so fundamental neue Weise, dass selbst Heisenberg zunächst zögert die Arbeit zu veröffentlichen. Zurück in Göttingen bespricht er die neuen Erkenntnisse mit seinem erfahrenen Kollegen Max Born. Dieser erkennt sofort die Tragweite der neuen Ideen. Zusammen arbeiten sie, mit Unterstützung von Borns Student Pascual Jordan, die ganze Quantenmechanik in einer Serie von drei Aufsätzen aus ^vii.

Heisenbergs erste Arbeit wurde später als „magischer Aufsatz“ bezeichnet ^viii: Zu Heisenbergs Zeit war nur wenig über die Welt der Atome bekannt. Und trotzdem schaffte er es mit nahezu schlafwandlerischer Sicherheit die Grundidee der Quantenmechanik in wenigen Zeilen herzuleiten: Die Umformulierung der Physik über den abstrakten Hilbertraum.

Im zweiten Aufsatz stellte das Team dann die Unschärferelation vor ^ix:

Um einen Eindruck von der Unschärferelation zu bekommen, kommen wir noch mal auf unser Zauberer-Beispiel zurück. Wir hatten gesehen, dass Darcy Oake die Zustände „Kameramann“ und „Zauberer auf dem Podest“ gleichzeitig besitzt. Angenommen er hat noch zwei andere Zustände „Alt“ und „Jung“, die er ebenfalls gleichzeitig besitzt. Die vier Eigenschaften hängen aber auf überraschende Weise voneinander ab:

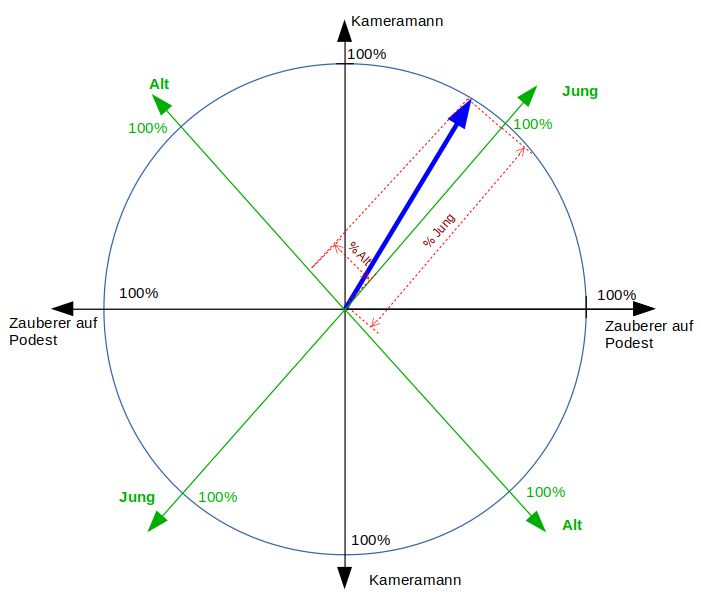
„Kameramann“ und „Zauberer auf dem Podest“ hatten wir mit den beiden Achsen im Zeigerdiagramm gleichgesetzt. „Alt“ und „Jung“ sollen auch zwei Achsen in demselben Zeigerbild bekommen. Aber um 45° gedrehte Achsen! Das Thema hatten wir schon mal beim Hadamard-Quantengatter.

Für das Qubit-Beispiel von oben messen die Assistenten also mit fast 100%-iger Wahrscheinlichkeit den Zustand „Jung“ und nur selten den Zustand „Alt“.

Wenn jetzt ein Assistent den Zustand „Jung“ für Darcy Oake misst, dreht er damit das Zauberer-Qubit auf die grüne „Jung“-Achse. Aber was ist mit den Zuständen „Kameramann“ und „Zauberer auf dem Podest“?

Die sind jetzt komplett ungewiss!

Das Zauberer-Qubit steht jetzt genau in der Mitte zu den anderen beiden Achsen „Kameramann“ und „Zauberer auf dem Podest“. Eine Messung ergibt jetzt zu 50% den Kameramann und zu 50% den Zauberer auf dem Podest. Sobald ein Assistent jetzt zum Beispiel den Zustand Kameramann misst, dreht sich das Zauberer-Qubit auf die Kameramann-Achse.

Jetzt ist aber wieder die Messung für „Jung“ und „Alt“ komplett ungewiss!

Was jetzt auch klar wird: Es macht sogar einen Unterschied, ob die Assistenten zuerst die Messung für „Jung“ oder „Alt“ und danach die Messung für „Kameramann“ oder „Zauberer auf dem Podest“ durchführen oder umgekehrt!

Die Heisenbergsche Unschärferelation sagt jetzt Folgendes aus: Das gleiche Prinzip gilt in der Quantenwelt für den Ort und den Impuls, also die Geschwindigkeit, eines Teilchens. Der Ort ist wie die Zustände „Kameramann“ und „Zauberer auf dem Podest“ (nur wieder mit viel viel mehr senkrechten Achsen), der Impuls wie die Zustände „Jung“ und „Alt“. Wenn wir den Ort genau kennen, hat sich der Quanten-Zeiger des Teilchens so in die Mitte der Impuls-Achsen gedreht, dass der Impuls komplett ungewiss geworden ist. Andersherum gilt das Gleiche: Wenn wir den Impuls genau kennen, können wir nichts mehr über den Ort des Teilchens aussagen. Für beide Größen kommen wir an einer Unschärfe nicht vorbei.

Außerdem macht es einen Unterschied, ob wir zuerst den Ort und danach den Impuls messen oder umgekehrt. Die Messungen in der Quantenmechanik kann man also nicht einfach vertauschen und das gleiche kommt heraus. Deshalb nennt man die algebraischen Berechnungen in der Quantenmechanik auch „nichtkommutativ“. Warum die Natur sich gerade so verhält weiss bis jetzt kein Mensch. Aber auf diese Weise können die Physiker das Phänomen exakt beschreiben.

Nur wenn das Diagramm auf die Achsen für „Kameramann“ und „Zauberer auf dem Podest“ ausgerichtet ist, können wir die Wahrscheinlichkeiten für diese Zustände ablesen. Für die Zustände „Jung“ und „Alt“ gilt das zunächst nicht. Dafür müssen wir die Achsen erst auf die Sichtweise für „Jung“ und „Alt“ drehen. Der Wechsel zwischen den verschiedenen Sichtweisen auf ein Qubit oder auch auf ein Elektron nennt man „Basiswechsel“. Der Basiswechsel zwischen Ortsdarstellung und Impulsdarstellung hat einen speziellen Namen: Die „Fouriertransformation“. Ein Kernbaustein des Shor-Algorithmus ist z.B. auch die Fouriertransformation, die auf mehrere Qubits angewendet wird. Im Schaltdiagramm des Shor-Algorithmus auf der Quirk-Homepage unten erkennen Sie das an dem Kürzel „QFT“. Für ein Qubit ist die Fouriertransformation gerade das Hadamard-Quantengatter.

Fußnoten