Quantencomputer besitzen das Potential gewissse, zentrale Computer-Anwendungen extrem abzukürzen. Dazu zählen etwa atomare Simulationen, Optimierung. Maschinenlernen und Finanzmathematik. Ermöglicht wird dies durch die faszinierende Quantenlogik. Die Hersteller der ersten Quantencomputer stellen für diese andersartige Logik spezielle Programmier-Schnittstellen für herkömmliche Computer bereit. Wie so ein Quanten-Programm konkret aussieht, stelle ich Ihnen hier am Beispiel von IBMs Quantencomputer und dem berühmten Grover-Quantenalgorithmus vor.
Inhalt
- 1 Eine Idee wird geboren
- 2 Was ist ein Quantencomputer?
- 3 Quantencomputer programmieren: Die Quantengatter
- 4 Quantencomputer programmieren: Welche Programmiersprachen gibt es für Quantencomputer?
- 5 Quantencomputer progammieren: IBMs Python-API „Qiskit“
- 6 Quantencomputer programmieren: Der Grover Algorithmus
- 7 Quantencomputer programmieren: Unser erstes Qiskit-Programm
- 8 Fußnoten
Eine Idee wird geboren
Im tiefsten Inneren funktioniert die Natur nicht nach unseren Alltagsgesetzen, sondern nach den rätselhaften Gesetzen der Quantenwelt. Aus diesem Grund stoßen herkömmliche Computer schnell an ihre Grenzen, wenn es darum geht Naturprozesse im atomaren Maßstab zu berechnen. Vor über 30 Jahren hinterließ der legendäre Physiker Richard Feynman der Wissenschaftswelt ein visionäres aber nahezu aussichtsloses Vermächtnis: Erst wenn es uns gelänge Computer zu konstruieren, die auf eben dieser Quantenlogik basieren, könnten wir die Natur letztendlich effizient simulieren und grundlegend berechnen.
Im Laufe der Zeit kamen weitere Anwendungsgebiete hinzu, für die Quanten-Forscher, dank der Quantenlogik, extrem abgekürzte Rechenwege voraussagten. Zu diesen Anwendungen zählen etwa Optimierungsaufgaben. Maschinenlernen und Finanzmathematik. Einige der Quanten-Algorithmen, die dafür gefunden wurden, stelle ich meinen Artikel „Anwendungen für Quantencomputer“ genauer vor.
Was ist ein Quantencomputer?
Was ist nun das Besondere an der Quantenlogik?
Nehmen wir z.B. den elementaren Baustein für herkömmliche Computer: Dem Bit. Ein Bit ist ein elektronischer An- / Ausschalter, dem man einfach die Werte 1 und 0 zuschreibt. Die Kombination vieler Bits ermöglicht nun beliebige Daten zu speichern und zu verändern.
In der Welt der Quantencomputer spricht man nicht von Bits, sondern von „Quanten-Bits“ bzw. „Qubits“. Genauso wie herkömmliche Bits können Qubits die Werte 0 oder 1 annehmen. Darüber hinaus können sie sich aber auch in „überlagerten“ Zuständen von sowohl 0 als auch 1 befinden.
Um dies zu veranschaulichen, verwende ich auf „quantencomputer-info.de“ eine Qubit-Darstellung, die gegenüber der Lehrbuchdarstellung vereinfacht ist aber dem Kern bereits sehr nahe kommt: Ein einfacher Zeiger in einer Ebene. Folgendes Qubit ist zum Beispiel zu gleichen Teilen sowohl im Zustand 0 als auch im Zustand 1.
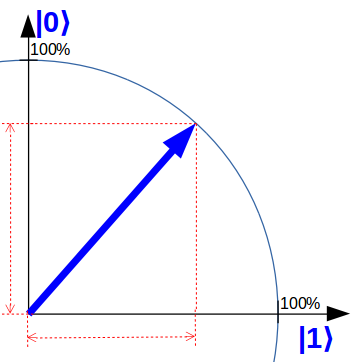
Im Verlauf einer Quantencomputer-Programms werden die Qubits durch den Einsatz von sogenannten „Quantengattern“ gedreht und am Ende ausgemessen. Durch diese Messung „entscheiden“ sich die Qubits jeweils für einen der beiden Werte: 0 oder 1. Diese Entscheidung geschieht am Ende zufällig und unterliegt den Gesetzen der Quantenmechanik. Die Kunst besteht nun darin, diese Wahrscheinlichkeitsverteilung gezielt zu steuern: Im Verlaufe dieses Artikels werden Sie einen genauen Eindruck davon bekommen.
Der eigentliche Clou der Qubits ist Folgender: Ein Quantencomputer verdoppelt seine potentielle Rechenstärke mit jedem zusätzlichen Qubit. Also exponentiell!
Noch viel mehr über die fundamentalen Unterschiede zwischen einem herkömmlichen Computer und einem Quantencomputer erfahren Sie in meinem Einstiegsartikel „Der unglaubliche Quantencomputer einfach erklärt“.
Vor gut zwei Jahrzehnten fingen auch die Tech-Riesen an, sich mit der neuen Technologie zu befassen. Der Bau von leistungsstarken Quantencomputern ist eine Herkulesaufgabe, bei der wir noch ganz am Anfang stehen. Allerdings stehen mittlerweile die ersten Quantencomputer-Angebote von Tech-Firmen in der Cloud bereit. Verfügbar für jedermann. Den aktuellen Stand beschreibe ich in meinem Artikel „Welche Quantencomputer gibt es jetzt schon?“.
Die aktuellen Quantencomputer befinden sich noch in der sogenannten „NISQ-Ära“. Das steht für „Noisy Intermediate Scale Quantum“, also fehleranfällige Quantencomputer mit einer „mäßigen“ Größe von höchstens wenigen Hundert „Qubits“, perspektivisch gesehen. Voraussichtlich wird es noch einige Jahre dauern, bis die Technologie soweit skaliert ist, um von direktem gesellschaftlichen Nutzen zu sein. Aber schon jetzt bauen die Hersteller ihre gesamte Infrasktruktur aus und vielversprechende Quanten-Algorithmen können direkt erforscht und erprobt werden.
Dass allerdings selbst mit einem NISQ-Quantencomputer ein exponentieller Quantenvorteil gegenüber herkömmlichen Supercomputern möglich ist, bewies Google zuletzt eindrucksvoll. Die Details dazu erläutere ich in meinem Artikel „Google und der Nachweis der Quanten-Überlegenheit“.
Quantencomputer programmieren: Die Quantengatter
Die zentralen Bausteine von Quantenprogrammen sind, neben den Qubits, die „Quantengatter“.
Herkömmliche Computer bilden unsere Alltagslogik durch sogenannte UND-, ODER-, NICHT-Gatter ab. Diese Gatter manupilieren die Bits und bilden somit die fundamentalen Bausteine von herkömmlichen Computerprogrammen. Die Quantenlogik wiederum bildet ein Quantencomputer durch völlig andersartige „Quantengatter“ ab.
Um die Quantencomputer einem breiteren Publikum näher zu bringen, verwende ich auf „quantencomputer-info.de“ eine vereinfachte Sichtweise auf die Qubits und die Quantengatter. In meinem Artikel Das Qubit und ein Magier bei „Britain Has Got Talent“ hatte ich schon die Zeigerbilder eingeführt mit denen wir uns die verschiedenen Zustände einesQubits vorstellen können. Das Qubit ist dann ein Zeiger auf der Kreislinie in diesem Bild.
(„Disclaimer“: In der Lehrbuch-Darstellung liegt die Zeigerspitze eines Qubits im Gegensatz dazu auf einer Kugeloberfläche: Die „Blochkugel“ i. Um das Quanten-Programm für den Grover-Algorithmus richtig zu verstehen, reicht meine einfache Sichtweise mit der Kreislinie aber erstaunlicherweise aus)
Folgendes Zeigerbild zeigt wieder ein Qubit, dass gleichzeitig im Zustand |0⟩ und im Zustand |1⟩ ist.
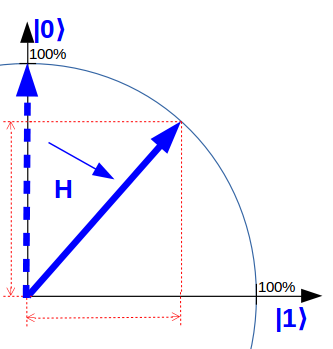
Das Besondere an diesem Bild ist außerdem, dass die Zustände |0⟩ und |1⟩ gleichmäßig überlagert sind. Es ist zu gleichen Teilen sowohl |0⟩ als auch |1⟩. Ein Qubit im Zustand |0⟩ gelangt in diesen Zustand der gleichmäßigen Überlagerung, indem es in dem vereinfachten Zeigerbild um 45° gedreht wird. Diese Drehung wird durch das Hadamard-Quantengatter H durchgeführt.
|qubit⟩ = H |0⟩
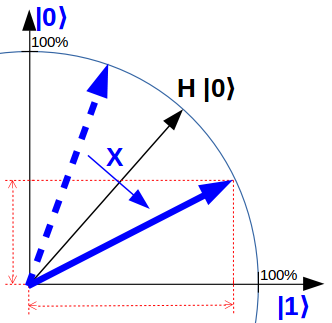
Ein anderes Gatter ist das X – Quantengatter. Es spiegelt das aktuelle Qubit an der Winkelhalbierenden, also gerade am Zustand H |0⟩. Oder anders betrachtet: Das X-Gatter tauscht den Zustand |0⟩ und den Zustand |1⟩ gegeneinander aus.
X |0⟩ = |1⟩ und X |1⟩ = |0⟩
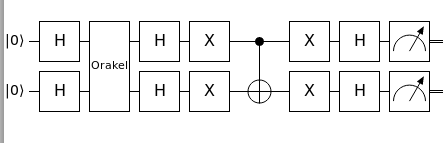
Ein Quantenprogramm besteht nun aus mehreren hintereinander geschalteten Quantengattern. Am Ende eines Quantenprogramms werden alle Qubits ausgelesen und als Resultat erhält man eine Bit-Sequenz von 0en und 1en. Folgendes Beispiel zeigt ein Schaltdiagramm für den Grover-Algorithmus für zwei Qubits. Wir werden den Grover-Algorithmus weiter unten für drei Qubits programmieren.
Quantencomputer programmieren: Welche Programmiersprachen gibt es für Quantencomputer?
Um ein Quantenprogramm durchzuführen, muss ein Quantencomputer eine Serie von Quantengattern auf bestimmte Qubits ausführen. Schematisch wird das durch Schaltdiagramme symbolisiert, wie in dem Beispiel oben. Eine Programmiersprache für Quantencomputer muss also in der Lage sein, solche Diagramme programmatisch abzubilden.
Prinzipiell wäre jede Programmiersprache für herkömmliche Computer dazu in der Lage. Die Besonderheit hierbei ist lediglich, dass die Sprache Bausteine für die einzelnen Quantengatter bereitstellen muss. Der Quantencomputer muss dann für diese Bausteine einen Treiber zur Verfügung stellen, der die Quantengatter-Anweisung in eine physikalische Quanten-Schaltung übersetzt.
In einem supraleitenden Quantencomputer wird ein H-Quantengatter etwa durch einen Mikrowellenimpuls mit einer genau-dosierten Impulslänge realisiert, Dieser zielt auf einen supraleitenden Schwingschaltkreis: Dem physikalische Qubit. Für aktuelle Quantencomputer nimmt die externe Steuer- und Ausleseelektronik nebenbei den größten Platz ein. Um dies zu reduzieren, gibt es Bestrebungen die Steuerung in eine Platine direkt in den Quantencomputer zu verlagern ii.
Als Programmiersprache für Quantencomputer hat sich die beliebte Programmiersprache „Python“ für herkömmliche Computer herauskristalisiert. Die Hersteller von Quantencomputern stellen hierfür eine Programmierschnittstelle (bzw. eine API) zur Verfügung, die die benötigten Erweiterungen bereitstellt. Der Quantencomputer wird darüber von einem lokalen herkömmlichen Arbeitsplatzrechner ferngesteuert: Das fertige Programm wird über die Schnittstelle / API an den Quantencomputer gesendet, der den Programmauftrag in eine gemeinsame Warteschleife für den Quantencomputer stellt. Sobald die nötigen Ressourcen frei sind, führt der Quantencomputer das Quantenprogramm aus und sendet das Ergebnis an den lokalen Arbeitsplatz zurück.
Um diesen Ablauf abzukürzen besitzen alle APIs sogenannte Quantencomputer-Simulatoren. Diese laufen nur auf dem lokalen Arbeitsplatzrechner. Da herkömmliche Computer einen Quantencomputer nur bedingt simulieren können, kann man über die Simulatoren nur Quantenprogramme mit wenigen Qubits austesten.
Quantencomputer progammieren: IBMs Python-API „Qiskit“
IBM ist einer der Pioniere in der Quantencomputer–Entwicklung. Entsprechend verwundert es nicht, dass der Techriese der erste Hersteller war, der 2015 einen 5 Qubit-Quantencomputer als Cloudangebot zur Verfügung stellte. Mittlerweile bietet IBM in seinem Cloudangebot „IBM Quantum Experience“ weitere Quantencomputer auf Supraleiter-Basis mit bis zu 20 Qubits an iii. Mit einem Credit-System können Nutzer hierfür Quantenprogramm einstellen. Dabei stellt IBM die Dienste teilweise sogar kostenlos zur Verfügung.
Teil des Cloudangebotes ist die Python API „Qiskit“. Hierfür stellt IBM eine umfangreiche Dokumentation zur Verfügung iv. Probleme und Fragen rund um Qiskit können entweder über IBMs „Qiskit Slack“ oder über die unabhängige Website „Quantum Computing Stack Exchange“ gestellt werden v. Qiskit ist Open Source und das Projekt wird auf Github gehostet. IBM veranstaltet regelmäßig Events und „Hackathons“ für die API.
Um weitere Zusatzmodule für Python auf dem eigenen Arbeitsplatz einzubinden, stellen die Entwickler der Programmiersprache Python den Packagemanager „pip“ zur Verfügung. Mit folgenden Anweisungen installieren Sie zum Beispiel Python 3 und Pip für einen Linux Ubuntu 18.04 Arbeitsplatz:
sudo apt-get install python3-pip
Sobald „pip“ installiert ist kann Qiskit als Zusatzmodul eingebunden werden
python3 -m pip install –user qiskit
Um ein Python / Qiskit – Programm zu schreiben, reicht ein einfacher Texteditor aus. Per Kommandozeile kann die erstellte Datei (z.B. „programm.py“) dann in einer DOS- oder Linux-Shell ausgeführt werden.
python3 programm.py
Komfortabler macht man es sich, wenn man hierfür eine „Entwicklungsumgebung“ verwendet. Darüber sind diverse Zusatzfunktionen, die bei der Programmierung hilfreich sind, direkt verfügbar. Als eine der Standardumgebung (für wissenschaftliche Programmierung mit Python im Allgemeinen und für die Programmieren von Quantencomputern im Besonderen) hat sich die freie Umgebung „Jupyter Notebook“ bewährt vi.
Ein Jupyter-Notebook kann in einem beliebigen Browser (Chrome, Firefox, IE, …) bearbeitet werden und wird dort auch ausgeführt. Nebenbei kann ein Jupyter Notebook Markup-Texte, Bilder und wissenschaftliche Formeln direkt einbinden.
Folgender Befehl installiert etwa die nötigen Jupyter-Packages auf einem lokalen Linux Ubuntu – Arbeitsplatz:
python3 -m pip install –user ipython jupyter
Danach starten Sie Jupyter Notebook über den Kommandozeilen-Befehl
jupyter notebook
Noch einfacher machen Sie es sich, wenn Sie dies alles zusammen in der Python-Distribution „Anaconda“ installieren vii. Anaconda ist für sämtliche Betriebssysteme verfügbar und hat sich zu einem Standard im Data Science – und Machine-Learning- Umfeld entwickelt. Darüber hinaus stellt Anaconda diverse weitere Tools für das wissenschaftliche Arbeiten mit Daten und für das Machine-Learning zur Verfügung.
Quantencomputer programmieren: Der Grover Algorithmus
In diesem Artikel werden wir mit Qiskit ein Quantenprogramm für den berühmten Grover-Algorithmus erstellen. Das Quantengatter-Schaltdiagramm hatten Sie bereits oben kurz kennengelernt. Der Grover-Algorithmus ist ein universeller Quanten-Algorthmus für sämtliche „Nadel-Im-Heuhaufen“-Probleme. Dazu zählen übrigens auch Optimierungsprobleme. Gegenüber herkömmlichen Computern beschleunigt der Grover-Algorithmus die Ausführungszeit quadratisch: Benötigt ein herkömmlicher Computer für die Lösung des Problems 1 Millionen Durchläufe, so benötigt der Grover-Algorithmus nur etwa 1000 Durchläufe.
Sie erinnern sich, dass das Endergebnis eines Quanten-Programms per Messung aus den Qubits ausgelesen wird. Dabei bedingt die Quantenmechanik, dass es vom Zufall abhängt, ob ein Qubit am Ende den Wert 0 oder den Wert 1 zurückgibt. Der Clou des Grover-Algorithmus besteht nun darin, dass das gesuchte Ergebnis (in Form von einer Bit-Sequenz z.B. „0 0 1 0 1 1 0 ….“) mit jedem Durchlauf weiter verstärkt wird. Im Gegensatz dazu werden die „falschen“ Bit-Sequenzen immer weiter unterdrückt. Weiter unten werden sie ein genaues Bild davon bekommen.
Wir beschränken uns hier darauf das obige Schaltbild für drei Qubits zu programmieren. Den Grover-Algorithmus selbst stelle ich im Detail in dem Artikel „Der Grover-Algorithmus und die Suche nach dem heiligen Gral“ vor. Um die Funktionsweise des Algorithmus zu verstehen, empfehle ich Ihnen diesen zu lesen.
Quantencomputer programmieren: Unser erstes Qiskit-Programm
Im Folgenden sehen Sie unser Quantenprogramm, wie es sich in Jupyter Notebook darstellt. Die einzelnen Zellen klammern lediglich bestimmte Programmteile. Wir hätten hierfür auch ein einzelnes Skript bzw. eine einzelne Zelle verwenden können.
Auf „Google Colaboration“ habe ich das Quantenprogramm ebenfalls für Sie bereitgestellt:
https://colab.research.google.com/drive/1bTGLjxU33yWqKAVI5LCudf-jqdlsVy-l
Indem Sie dort auf „Open Playground“ klicken, können Sie es in einer Spielwiese selbst verändern und ausführen. Das Programm läuft dabei nicht bei Ihnen lokal, sondern auf den Google-Servern ab.
Der Grover-Algorithmus als Qiskit-Programm
Auch auf Google-Colaboration verfügbar:
https://colab.research.google.com/drive/1SchqSnnycmLpTSrs-ToUnC2zDpCjWgxs
# Pip-Anweisung, Qiskit nachzuinstallieren,
# falls noch nicht vorhanden
! pip3 install qiskit --quiet
! pip3 install qiskit-terra[visualization] --quiet
# Zunächst müssen wir die Qiskit-Module einbinden,
# die wir für das Quantenprogramm benötigen:
import qiskit
from qiskit import(QuantumCircuit, execute, Aer, BasicAer)
from qiskit.visualization import plot_histogram
from qiskit.visualization import plot_state_city
# Versionen der einzelnen Qiskit-Modulen ausgeben:
qiskit.__qiskit_version__
# Globale Variablen und Funktionen
# Anzahl von Qubits: 3
n = 3
# Folgende Quantenschaltungen werden wir abwechselnd
# wiederverwenden. Deshalb packen wir sie in eine Python-Funktion
# Die Quantenschaltung für das Oracle:
# Reflektiert alle Qubits am Zeiger auf die Lösung: (0,0,1)
# Was dabei nur schwer zu sehen ist:
# Dafür müssen wir die Lösung tatsächlich NICHT kennen
# ... glauben Sie es mir einfach!
def add_reflect_oracle(circuit):
circuit.h(2)
circuit.ccx(0,1,2)
circuit.h(2)
# Die Quantenschaltung für den Grover-Operator:
# Reflektiert alle Qubits am Zeiger auf den Zustand
# der gleichförmigen Überlagerung s = (1, 1, 1)
def add_reflect_s(circuit):
for i in range(n):
circuit.h(i)
for i in range(n):
circuit.x(i)
circuit.h(2)
circuit.ccx(0,1,2)
circuit.h(2)
for i in range(n):
circuit.x(i)
for i in range(n):
circuit.h(i)
Als Qiskit-Programm werden wir den Grover-Algorithmus jetzt jeweils 0 bis 4 Grover-Durchläufe ausführen. Dabei werden wir jeweils das Quanten-Schaltung und die Messergebnisse als Diagramm ausgeben. Dabei werden Sie erkennen wieviel Durchläufe der Grover-Algorithmus benötigt, um ein optimales Ergebnis zu liefern.
Grover-Algorithmus mit 0 Durchläufen
# Ab hier startet das eigentliche Quantenprogramm:
# Zunächst muss ein "Backend" festgelegt werden
# Unser Backend ist ein Quantencomputer-Simulator:
simulator = Aer.get_backend('qasm_simulator')
#simulator = BasicAer.get_backend('statevector_simulator')
# Wir wollen einen Quanten-Schaltkreis
# mit n=3 Qubits erstellen:
circuit = QuantumCircuit(n, n)
# Wir überführen jedes Qubit i in den
# Zustand der gleichförmigen Überlagerung:
for i in range(n):
circuit.h(i)
# Für 0 Durchläufe lassen wir die Schaltungen für die
# Reflektionen weg.
# Am Ende Messen wir die Qubits aus
circuit.measure(range(n), range(n))
# Einer der Vorzüge von Qiskit: Die Visualisierungen!
# "Magic Function" für IPython / Jupyter
# Anweisung damit Bilder direkt angezeigt werden
%matplotlib inline
# Zeichnet das Diagramm zu unserem Quanten-Schaltkreis
# direkt im Jupyter Notebook
# Außerhalb vom Notebook muss das Image extern abgelegt
# werden mit dem Parameter filename="my_circuit.png"
# Hierbei sind diverse Datentypen möglich
circuit.draw(output="latex")
# output-Typen sind "text", "mpl", "latex", "latex_source"
# Den "Job" wiederholen wir 1000 Mal und lassen
# Qiskit ein Diagramm über die Statistik der zeichnen
job = execute(circuit, simulator, shots=1000)
result = job.result()
plot_histogram(result.get_counts(circuit))
Gleichverteilung: Nach 0 Grover-Durchläufen hat der
Grover-Algorithmus das gesuchte Ergebnis noch nicht
verstärkt.
Grover-Algorithmus mit 1 Durchlauf
# Schaltkreis nochmal neuerstellen,
# ausmessen und Diagramme ausgeben
circuit = QuantumCircuit(n, n)
for i in range(n):
circuit.h(i)
# 1 Grover-Durchlauf
add_reflect_oracle(circuit)
add_reflect_s(circuit)
circuit.measure(range(n), range(n))
circuit.draw(output="latex")
job = execute(circuit, simulator, shots=1000)
result = job.result()
plot_histogram(result.get_counts(circuit))
Nach einem Grover-Durchlauf hat der Algorithmus die Lösungssequenz 1 1 1 schon deutlich verstärkt.
Grover-Algorithmus mit 2 Durchläufen
# Schaltkreis nochmal neuerstellen,
# ausmessen und Diagramme ausgeben
circuit = QuantumCircuit(n, n)
for i in range(n):
circuit.h(i)
# 2 Grover-Durchläufe
add_reflect_oracle(circuit)
add_reflect_s(circuit)
add_reflect_oracle(circuit)
add_reflect_s(circuit)
circuit.measure(range(n), range(n))
circuit.draw(output="latex")
job = execute(circuit, simulator, shots=1000)
result = job.result()
plot_histogram(result.get_counts(circuit))
Nach zwei Grover-Durchläufen hat der Algorithmus die Lösungssequenz 1 1 1 fast vollständig verstärkt.
Grover-Algorithmus mit 3 Durchläufen
# Schaltkreis nochmal neuerstellen,
# ausmessen und Diagramme ausgeben
circuit = QuantumCircuit(n, n)
for i in range(n):
circuit.h(i)
add_reflect_oracle(circuit)
add_reflect_s(circuit)
add_reflect_oracle(circuit)
add_reflect_s(circuit)
add_reflect_oracle(circuit)
add_reflect_s(circuit)
circuit.measure(range(n), range(n))
circuit.draw(output="latex")
job = execute(circuit, simulator, shots=1000)
result = job.result()
plot_histogram(result.get_counts(circuit))
Wir erkennen also, dass der Grover-Algorithmus nach
zwei Durchläufen das beste Ergebnis liefert und danach wieder
schlechtere Werte. Das Ganze verhält sich periodisch. Und genauso
erwarten wir es auch, wenn wir uns nochmal vergegenwärtigen, wie
der Grover-Algorithmus funktioniert.
Nur so nebenbei:
Die Quantengatter, die wir verwendet haben besitzen auch eine Matrix-Darstellung.
from qiskit.extensions.standard.h import HGate
HGate().to_matrix()
from qiskit.extensions.standard.x import XGate
XGate().to_matrix()
Am Ccx-Quantengatter erkennen Sie übrigens, das herkömmliche Computer schnell an ihre Grenzen
stoßen, wenn die Qubit-Anzahl zunimmt.
Das Ccx – / Toffoli – Quantengatter operiert gerade mal auf 3 Qubits.
Die Matrix ist aber schon jetzt unübersichtlich:
from qiskit.extensions.standard.x import ToffoliGate
ToffoliGate.to_matrix(ToffoliGate)
Fußnoten
i Das exakte Bild eines Qubits ist das einer Kugeloberfläche. Die Zustände |0⟩ und |1⟩ müssen wir dann an Nord- und Südpol einzeichnen. Um von der Kreislinie zur Kugeloberfläche zu gelangen, muss ein zusätzliche Winkel verwendet werden, der auch „Phase“ genannt wird.
ii https://t3n.de/news/quanten-computing-intel-gibt-1253925/: Artikel „Quanten-Computing: Intel gibt Details zum neuen Cryo-Chip Horse Ridge preis“ über Intels Steuerplatine für Mikrwowellenstrahlung, der in der Lage wäre innerhalb der Tieftemperatur-Umgebung eines Quantencomputers zu arbeiten.
iii https://quantum-computing.ibm.com/: Homepage von IBM Clouddienst „Quantum Experience“.
iv https://quantum-computing.ibm.com/docs/qis-tut/: Dokumentation für IBMs Python API „Qiskit“
v https://quantum-computing.ibm.com/support: Referenz-Seite zum „Qiskit Slack“ oder zu den entsprechenden Tags auf „Quantum Computing Stack Exchange“.
vi https://jupyter.org/: Homepage des Jupyter-Projektes. „Jupyter“ ist eine Namenskombination aus den drei Programmiersprachen Julia, Python, R, die eine wichtige Rolle bei der Programmierung im wissenschaftlichen Umfeld spielen.
vii https://www.anaconda.com/distribution/: Homepage der Python / R – Distribution „Anaconda“.
